Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 97

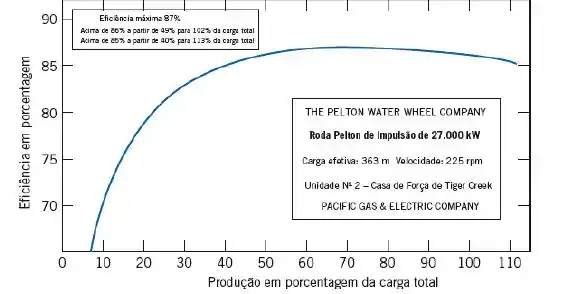
A figura 10.37 apresenta dados para a eficiência de uma grande roda de água Pelton instalada na Usina Hidrelétrica de Tiger Creek da Pacific Gas & Eletric Company, perto de Jackson, na Califórnia. Esta unidade tem potência nominal de 26,8 MW, quando operada a 225 rpm, sob uma altura de carga de água de 360 m. Adote valores razoáveis para ângulos de escoamento e coeficiente de perda no bocal e para a água a 15°C. Determine o diâmetro do rotor e estime o diâmetro do jato e a vazão mássica de água.

Passo 1

Tá legal! Vamos começar o exercício calculando a velocidade do jato para um sistema com perdas no bocal, então, temos:

V j = C v 2 g H

Agora, como o enunciado nos disse para adotar um valor para a perda no bocal, vamos utilizar C v = 0,98 , então, a velocidade do jato será:

V j = 0,98 2 ( 9,81 ) ( 360 ) → V j = 82,36   m / s

Agora, vamos utilizar a figura 10.36 para encontrar o raio do rotor, então, pegando a máxima eficiência do diagrama abaixo, temos:

U V j = 0,48 → U = 0,48 V j

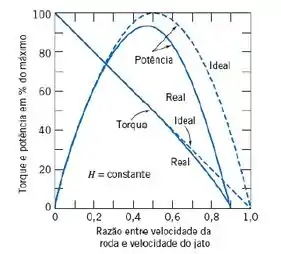
Substituindo o valor encontrado para V j temos:

U = 0,48 82,36 → U = 39,5   m / s

Passo 2

Agora, para encontrar o raio do rotor, podemos usar a relação entre a velocidade da roda, sua velocidade angular e o raio. A relação é:

U = ω R → R = U ω

Substituindo os valores conhecidos (lembrando de converter a rotação para radianos por segundo), temos:

R = 39,5 225 2 π 60 → R = 1,67   m

Sabemos que o diâmetro é duas vezes o raio, então:

D = 2 R = 2 1,67 → D = 3,34   m

Passo 3

Agora, do diagrama presente no enunciado, temos que a eficiência para uma carga total de 100% será:

η = 0,86

E, nós sabemos que o trabalho produzido pelo sistema pode ser escrito como:

W ú t i l = η Q ρ g H → Q = W ú t i l η ρ g H

Substituindo os valores conhecidos, temos:

Q = 26,8.10 6 0,86 999 9,81 360 → Q = 8,83   m 3 / s

Agora, com a vazão conseguimos encontrar o diâmetro do jato através de:

Q = V j A j = V j π D j 2 4

Substituindo os valores conhecidos, temos:

8,83 = 82,36 π D j 2 4 → D j = 0,37   m

Passo 4

E agora, podemos encontrar a vazão mássica do sistema, também usando a vazão obtida no passo 3:

m ˙ = ρ Q

Substituindo os valores conhecidos:

m ˙ = 999 8,83 → m ˙ = 8821,2   k g / s

Resposta

D = 3,34   m

D j = 0,37   m

m ˙ = 8821,2   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pump, geometrically similar to the 12.95-in model inFig. P11.24, has a diameter of 24 in and is to develop 30 hpat BEP when pumping gasoline (not water). Determine(a)the appropriate speed, in r/min;
A centrifugal pump has r2 5 9 in, b2 5 2 in, and β2 5 358and rotates at 1060 r/min. If it generates a head of 180 ft,determine the theoretical (a) fl ow rate in gal/min and(b) horsepower. Assume near-
A 6.85-in pump, running at 3500 r/min, has the followingmeasured performance for water at 208C:Q, gal/min 50 100 150 200 250 300 350 400 450H, ft 201 200 198 194 189 181 169 156 139η, % 29 50 64 72 77
Apply the results of Prob. P11.95 to determine the optimum(a) penstock diameter and (b) nozzle diameter for a headof 330 m and a fl ow rate of 5400 m3/h with a cast ironpenstock of length 600 m.
The centrifugal pump of Fig. P11.21 develops a flowrate of 4200 gal/min of gasoline at 208C with near-radialabsolute inflow. Estimate the theoretical (a) horsepower,(b) head rise, and (c) appropriate