Em unidades típicas dos Estados Unidos, a definição comum de velocidade específica para uma turbina hidráulica é dada pela Eq. 10.13b. Desenvolva uma conversão entre essa definição e outra verdadeiramente adimensional em unidades SI. Avalie a velocidade específica de uma turbina de impulsão, operando a 400 rpm, sob uma altura de carga líquida de 1190 m com 86% de eficiência, quando suprida por jato único de diâmetro 6 mm. Use ambas as unidades, americanas e SI. Estime o diâmetro da roda.

Agora, para calcular as velocidades específicas, precisamos encontrar a potência produzida no sistema, cuja equação é:

Só que nós não temos a vazão, mas o enunciado nos forneceu o diâmetro do jato, então, se encontrarmos a velocidade do jato, encontramos a vazão. Dessa forma, sabemos que a velocidade do jato pode ser escrita como:

Substituindo os valores conhecidos:

Agora, a vazão será dada por:

Substituindo os valores conhecidos, temos:

Então, retornando a equação da potência apresentada no início desse passo, temos:

Agora podemos calcular a velocidade específica em unidades do sistema internacional através de:

Substituindo os valores conhecidos, temos:

Agora, precisamos converter os valores para utilizar a equação para o sistema dos Estados Unidos, então:

Então, substituindo os valores conhecidos na equação a seguir, temos:

Então o fator de conversão entre os dois sistemas pode ser obtido dividindo um pelo outro, dessa forma, temos:

Agora, para encontrar o diâmetro do rotor vamos recorrer ao seguinte gráfico apresentado nessa seção:

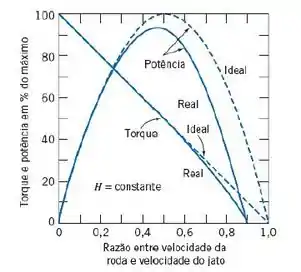
Nesse caso, como temos uma eficiência de 86%, então temos uma razão entre velocidade da roda e velocidade do jato como sendo:

Então, substituindo a velocidade do jato encontrada passo 2, temos:

E, sabemos que a velocidade da roda pode ser escrita em função do raio e da velocidade angular, então, temos:

Então o diâmetro do rotor será: