Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 117
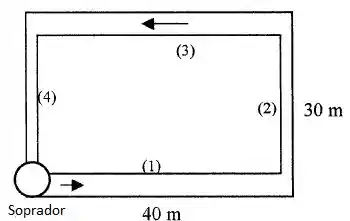
Um soprador fornece ar a 3000 m³/h ao circuito de dutos da figura abaixo. Todos os dutos são de aço comercial e de seção transversal quadrada, com lados e . Admitindo o ar em condições ao nível do mar, estime a potência necessária, considerando um rendimento de 75% para o soprador. Despreza as perdas localizadas.
Passo 1
Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!
Primeira coisa que vamos fazer é pegar as propriedades do ar.
Segunda coisa é entender o que ele está pedindo no problema! A potência que é dada como:
E perceba que a perda de carga ela será dada apenas pelas perdas de cargas maiores que são dadas por
Então precisamos das velocidades em cada uma das seções do nosso sistema e também de seus fatores de atrito.
Passo 2
Vamos estabelecer agora as velocidades em cada uma das seções, porque como estamos em um regime estacionário, temos que a vazão deve ser mantida em todo o sistema.
Como as seções são quadradas e os pares 1 e 3 possuem lado de mesmo tamanho, suas áreas transversais de escoamento também serão iguais e por consequência sua velocidade e Re.
O mesmo se aplica para os pares 2 e 4
Passo 3
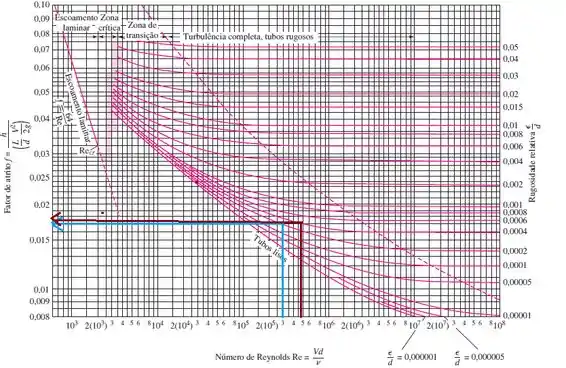
O aço comercial tem rugosidade (tabela 6.1 do livro) ! Olha que maravilha então, temos os comprimentos característicos de cada um dos dutos e sua rugosidade. De combo ainda temos os Reynolds de cada uma seção também, então agora é fácil calcularmos o fator de atrito, certo? Basta calcularmos a rugosidade relativa e olhar no diagrama de Moody!!!
Passo 4
Uma vez encontrado os fatores de atrito, calculamos a queda de pressão em cada seção:
Passo 5
A potência resultante do soprador então é: