Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas para exames de fundamentos de engenharia - Ex. 3

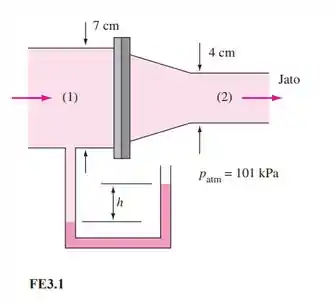
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se a velocidade é e o atrito é desprezado, qual é a força axial no flange, necessária para manter o bocal fixado ao tubo 1?

(a) 11 N, (b) 56 N, (c) 83 N, (d) 123 N, (e) 110 N

Passo 1

Para calcular a força axial no flange vamos precisar fazer uma análise da quantidade de movimento para o seguinte volume de controle em vermelho:

Olhando para o volume de controle vemos que em 1 o fluxo entre no volume de controle e em 2 o fluxo sai, sendo assim, de forma simples, o que entra é negativo e o que sai é positivo para quantidade de movimento. Como possuímos apenas movimento no eixo x, não vamos precisar analisar nada em y, sendo assim, o fluxo de quantidade de movimento em x na entrada do volume de controle é e na saída é .

Vamos fazer agora um balanço das forças no volume de controle. Como disse ali em cima, vamos analisar apenas em x, logo:

Estas são as forças em x, representa a força axial no flange e é o que estamos procurando. Ela possui aquele sinal de menos na frente porque é uma força oposta ao fluxo (adotei esse o sentido positivo de x). representa o termo de força exercida na seção transversal onde está localizada o flange.

Agora é só lembrar que e substituir:

Isolando :

Agora vamos precisar encontrar , e .

Passo 2

Começando com a vazão mássica ().

Este parâmetro é um pouco mais simples de encontrarmos pois:

Como o fluido escoando é a água, . Para a vazão nós podemos usar a velocidade 2 que foi dada no problema e a área de seção transversal em 2 (só usar o diâmetro ):

Com isso:

Passo 3

Para encontrar o valor de nós temos que usar vazão volumétrica de 2, que pela equação da continuidade é a mesma que em 1, ou seja, , e o diâmetro (), sendo assim:

Passo 4

Para o valor de vamos utilizar Bernoulli:

Vamos adotar que o ponto 1 e o ponto 2 estão na mesma altura, ou seja, , segundo, como é a pressão atmosférica, vamos assumir que porque dessa maneira já vamos encontrar direto a pressão manométrica em 1. Equacionando: