Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 110
Encontrou-se espaço para a instalação de um difusor cônico, com comprimento de 0,45 m, no sistema de ventilação da sala limpa descrito no Problema 8.106. O melhor difusor com este comprimento deve ser empregado. Considere que os dados da Fig. 8.16 possam ser usados. Determine o ângulo apropriado do difusor e a razão de áreas para esta instalação e estime a vazão volumétrica que será fornecida após a instalação do difusor.
Passo 1
Neste problema o sistema descrito no Problema 8.106 terá o acréscimo de um difusor. O que é pedido é o ângulo e a razão de áreas do difusor, bem como a vazão volumétrica fornecida após a sua instalação.
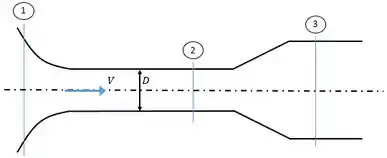
Três seções de avaliação será considerada sendo que aplicando a Equação da Energia entre as seções 1 e 3 tem-se que:
Sendo a perda definida como:
E a perda de carga do difusor (Eq. 8.42):
Sendo que:
E pela Eq. 8.41 que:
Como parâmetros e hipóteses foram fornecidos:
- regime permanente ();
- escoamento horizontal ();
- escoamento incompressível ( e );
- ;
- ;
- (ar na câmara praticamente parado);
- (foi dado aumento de pressão em termos de altura de água, por isso o uso a expressão de pressão estática);
- ;
- ;
- .
Passo 2
Aplicando a Equação da energia entre as seções 1 e 3:
Rearranjando a expressão acima:
Sabendo que , e :
Passo 3
A partir da equação da continuida pode-se escrever como função de :
Mas:
De forma que:
Passo 4
Assim, pode-se escrever a queda de pressão como:
Então a velocidade é dada por:
É conhecido a que de pressão em termos da pressão estática:
Assim:
Passo 5
As características do difusor podem ser obtidas a partir da Figura 8.16 considerando os parâmetros (note que é comprimento do difusor) e .
Sendo:
Graficamente pode afirmar que:
Passo 6
A velocidade será dada por:
Nota: para entrada bem arredonda pode-se afirmar que
Passo 7
A vazão será obtida por:
A vazão fornecida após a instalação do difusor será: