Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 43

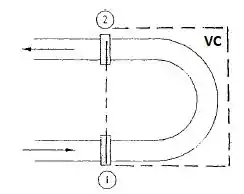
Água a 20°C escoa através de um tubo de 5 cm de diâmetro com uma curva vertical de 180°, como a figura abaixo. O comprimento total do tubo entre os flanges 1 e 2 é de 75 cm. Quando a vazão em peso é de 230 N/s, tem-se p 1 = 165   k P a e p 2 = 134   k P a . Desprezando o peso do tubo, determine a força total que os flanges devem suportar para esse escoamento.

Passo 1

Vamos fazer nosso volume de controle de forma que a gente consiga pegar os flanges do nosso equipamento, beleza?

Bem, precisamos analisar que o balanço de forças na direção x será dado por:

F x , f l a n g e + F p 1 + F p 2 + m ˙ 1 u 1 - m ˙ 2 u 2 = 0

Lembre-se que a força de pressão é dada F p = p A

Em todos os lados do volume de controle temos a pressão atmosférica atuando, certo? E se analisarmos as pressões aplicadas em cima e embaixo se cancelarão. Porém, note que os únicos pontos onde a pressão atmosférica não foi cancelada é na altura por onde entra e sai fluido, ou seja, precisamos nesses pontos descontar a pressão atmosférica quando formos abrir a força de pressão.

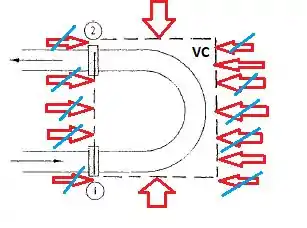
F x , f l a n g e + p 1 - p a t m A 1 + p 2 - p a t m A 2 = m ˙ 2 u 2 - m ˙ 1 u 1

Passo 2

A vazão mássica de entrada e saída deve ser igual, uma vez que estamos tratando de um fluido incompressível:

m ˙ = 230 N s g = 230 9,81 = 23,45   k g / s

A vazão volumétrica, podemos calcular como sendo:

Q = 23,45 k g s x 1 ρ = 23,45 979 = 0,0235   m 3 / s

Bem, olhando para nosso esquema no início da questão, observamos que não há mudança da área transversal de escoamento, ou seja, a vazão volumétrica vai se manter e por consequência a velocidade também será igual.

V 1 = V 2 = Q A = 0,0235 π 4 0,05 2 = 12   m / s

A 1 = A 2 = A = π 4 D 2

A velocidade de escoamento será igual a velocidade calcula acima, porém precisamos lembrar dos sinais quando estamos falando de um balanço de forças.

u 2 = - 12 m s

u 1 = 12 m s

Passo 3

Substituindo então os valores na nossa equação de balanço de força, temos:

F x , f l a n g e + π 4 0,05 2 165000 - 101325 + 134000 - 101325 = 23,45 - 12 - 12

F x , f l a n g e = - 126 - 65 - 561 = - 750   N

Passo 4

Analogamente, fazendo um balanço de forças na direção y, vamos ter que:

∑ F y = F y , f l a n g e = W t u b o + W f l u i d o

Onde W é a força peso! O enunciado diz que devemos desprezar o peso do tubo, então o peso do fluido é o que irá implicar na força, logo F y ,   f l a n g e = W f l u i d o = m g = ρ V g

F y , f l a n g e = ρ π 4 D 2 L g

Onde L é o comprimento do tubo, então temos que:

F y , f l a n g e = 979 x π 4 0,05 2 0,75 9,81 = 14 N

Resposta

F x , f l a n g e = - 750   N

F y , f l a n g e = 14   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.100 A velocidade horizontal na esteira atrás de um objeto posicionado em uma corrente de ar de velocidade uniforme U é dada por u r = U 1 - cos 2 ⁡ π r 2 , r ≤ 1 u r = U , r1 Em que r é a coordenada
4.96 Água é descarregada a vazão de 0,3 m³/s por uma fenda estreita em um tubo de 200 mm de diâmetro. O jato resultante, horizontal e bidimensional, tem 1 m de comprimento e espessura de 20 mm, mas co
4.101 Um fluido incompressível escoa em regime permanente na região de entrada de um canal bidimensional de altura 2 h = 100m m e largua w = 25m m . A vazão é Q = 0,025m ³ / s ³ . Encontre a velocidad
4.102 Um fluido incompressível escoa em regime permanente na região de entrada de um tubo circular de raio R = 75m m . A vazão é Q = 0,1m ³ / s ³ . Encontre a velocidade unifrome U 1 na entrada. A dis
4.97 Água escoa em regime permanente através da curva de 90° do Problema 4.39. O escoamento na entrada está a p 1 = 185k P a (absoluta). O escoamento na saída é não uniforme, vertical e à pressão atmo