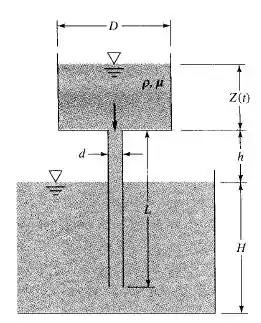
Vamos resolver o problema P6.25 na forma literal usando a figura abaixo. Todos os parâmetros são constantes, exceto a profundidade Z(t) do reservatório. Determine uma expressão para a vazão em função de . Estabeleça uma equação diferencial e resolva para o tempo de esvaziamento completo do reservatório superior. Admita escoamento laminar quase permanente.
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!
Vamos escrever nossa equação de balanço de forma geral:
Vamos agora olhar para os nossos pontos 1 e 2!!
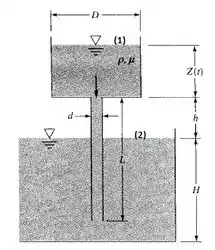
Se e , nossa equação se reduzirá em:
Sabe-se que
Então temos que:
Passo 2
O balanço de massa também dirá pra gente o seguinte:
Não temos nada “entrando” no nosso sistema, certo? Quando eu digo “sistema” estou falando do volume de controle igual fizemos ali para calcular nossa equação de energia, ou seja, nosso sistema é da superfície do tanque de cima até a superfície do tanque de baixo, beleza?
Então nosso balanço se reduzirá em:
Onde pela nossa equação encontrada no passo 1, sabemos que:
Passo 3
Vamos substituir então a velocidade e fazer separação de variáveis e depois integrar essa belezura!
Integrando essa belezura, vamos ter que:
Passo 4
O tanque estará drenado por completo quando tivermos que altura Z for igual a zero, certo?
Isso diz pra gente então que: