Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 90b

Água é bombeada à taxa de 0,075 m³/s de um reservatório que está 20 m acima de uma bomba para uma descarga livre 35 m acima da bomba. A pressão no lado da admissão da bomba é 150 kPa e no lado da descarga é 450 kPa. Todos os tubos são de aço comercial com diâmetro nominal de 15 cm. Determine (b) a perda de carga total entre a bomba e o ponto de descarga livre.

Passo 1

Considerando a Figura a seguir, este problema buscará obter a perda de carga entre as seções 3 e 4.

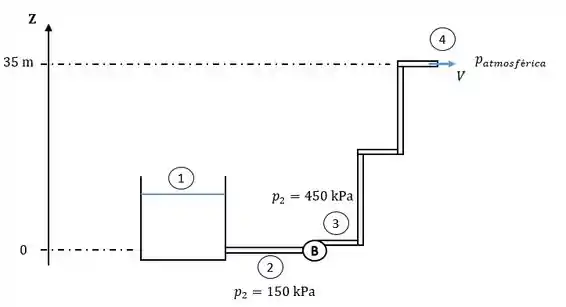
Para o cálculo da perda de carga será utilizada a Equação de Energia aplicada entre as seções 3 e 4, conforme expressão:

p 3 ρ 3 g + α V 3 2 2 g + z 3 = p 4 ρ 4 g + α V 4 2 2 g + z 4 + H l t

Para a aplicação da equação apresentada, as seguintes hipóteses são necessárias:

- regime permanente ( ∂ / ∂ t = 0 );

- escoamento incompressível ( ρ 3 = ρ 4 ,   ) e de água ( ρ = 1000   k g / m ³ );

- α ≈ 1,0 ;

- p 3 = 450   k P a ;

- p 4 = 0 (pressão atmosférica em termos manométrico);

- z 3 = 0 ;

- z 4 = 35   m

- Q = 0,075   m 3 / s ;

- tubo de seção constante ( V 3 = V 4 ).

Passo 2

A partir da Equação da Energia e buscando isolar o termo perda de carga:

p 3 ρ 3 g + α V 3 2 2 g + z 3 = p 4 ρ 4 g + α V 4 2 2 g + z 4 + H l t

H l t = p 3 ρ g - p 4 ρ g + α V 3 2 2 g - α V 4 2 2 g + z 3 - z 4

H l t = p 3 - p 4 ρ g + α V 3 2 - V 4 2 2 g + ( z 3 - z 4 )

Sabendo que V 1 = V 2 :

H l t = p 3 - p 4 ρ g + α × 0 + ( z 3 - z 4 )

Logo a perda de carga é dada por:

H l t = p 3 - p 4 ρ g + ( z 3 - z 4 )

Passo 3

Utilizando os parâmetros numéricos conhecidos:

H l t = p 3 - p 4 ρ g + ( z 3 - z 4 )

H l t = 450 × 10 3 - 0 1000 × 9,81 + ( 0 - 35 )

Assim, a perda de carga é de:

H l t = 10,9   m

Resposta

H l t = 10,9   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na instalação da figura, a potência trocada entre o fluido e a máquina é 7,14k W . Se o escoamento é perfeitamente isotérmico e o fluxo de calor dissipado entre 0 e e é 4,2k W , determinar:O tipo de m
No trecho 1 - ( 2 ) do conduto da figura, o escoamento do fluido ( γ = 8000N / m 3 ) é laminar, a vazão é 10L / s , o diâmetro é 8c m e o R e = 1000 . No trecho 3 - 4 o diâmetro é 6c m . O coeficiente
Uma bomba succiona água ( γ = 10000N / m 3 ) de um reservatório, cujo nível se encontra a 1,5m da sua seção de entrada, por um tubo de diâmetro de 50m m . Na saída da bomba encontra-se um manômetro me
No trecho 1 - ( 2 ) do conduto da figura, o escoamento do fluido ( γ = 8000N / m 3 ) é laminar, a vazão é 10L / s , o diâmetro é 8c m e o R e = 1000 . No trecho 3 - 4 o diâmetro é 6c m . O coeficiente
No escoamento por um tubo de um fluido muito viscoso, a perda de carga é dada por H P L = 51,87 π 1 π 2 , onde π 1 e π 2 são os adimensionais obtidos de Q = f D , g e v = f v , D , pelo teorema dos π