Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 10

A água contida no tanque (1) é descarregada através do bocal sem atrito. Seu nível h 1 pode ser considerado constante. O jato incide sobre uma placa de grandes dimensões que cobre a saída do bocal do tanque (2), contendo água a uma altura h 2 acima do orifício. Os bocais são iguais. Se h 2 for conhecido, determinar h 1 tal que a força do jato seja suficiente para anular a resultante das forças horizontais que agem sobre a placa.

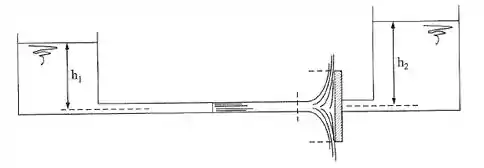
Passo 1

Para resolver esse exercício, precisamos igualar as componentes de força da esquerda e da direita que agem sobre a placa, para isso vamos usar a equação da força exercida pelo fluido, dada por:

F → s = - p 1 A 1 n → 1 + p p A p n → p + Q m v → p - v → 1

Passo 2

Vamos aplicar a equação na direção x ( → ) para o tanque da esquerda:

F s x = - - 0 A 1 0 + 0 A p 1 + Q m v p - 0

Então, a força da esquerda se resume a:

F s x e s q = Q m v p

Sabemos que:

Q m = ρ Q = ρ v p A

E, conseguimos encontrar v p (velocidade do jato) em função da altura do tanque, dada por:

v p = 2 g h 1

Substituindo esses dois valores na expressão, temos:

F s x e s q = ρ v p 2 A = ρ 2 g h 1 A

Passo 3

A força aplicada na placa pelo fluido do tanque da direita nada mais é do que a pressão manométrica exercida pelo pelo do fluido multiplicado pela área da placa, dado por:

F s x d i r = γ h 2 A = ρ g h 2 A

Igualando essa força com a força da esquerda, temos:

F s x e s q = F s x d i r

ρ ( 2 g h 1 ) A = ρ g h 2 A → h 1 = h 2 2

Resposta

h 1 = h 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro circular inserido através de uma corrente de água, conforme mostrado, deflete o escoamento de um ângulo θ . (Isto é chamado de “efeito Coanda”). Para a = 12,5m m , b = 2,5m m , V = 3m / s
Um tanque de água está apoiado dobre um carrinho com rodas sem atrito como mostrado. O carro está ligado a uma m = 10k g por meio de um cabo e coeficiente de atrito estático da massa com o solo é μ =
Uma placa vertical tem um orifício de bordas vivas no seu centro. Um jato de água com velocidade V atinge a placa concentricamente. Obtenha uma expressão para a força externa requerida para manter a p
Um trenó-foguete acelera do repouso sobre uma pista com resistências do ar e de rolamento desprezíveis. A massa inicial do trenó é m 0 = 600k g e o foguete contém inicialmente 150k g de combustível. O
Um trenó-foguete tem massa inicial de 5000k g , incluindo 1000k g de combustível. As resistências do ar e de rolamento na pista sobre a qual o trenó corre totalizam k u , em que k é 50N ⋅s / m e u é a