Um trenó-foguete tem massa inicial de , incluindo de combustível. As resistências do ar e de rolamento na pista sobre a qual o trenó corre totalizam , em que é e é a velocidade do trenó em . A velocidade de saída dos gases de combustão relativa ao foguete é de e a pressão de saída é atmosférica. A queima de combustível ocorre a uma taxa de .
- Trace o gráfico da velocidade em função do tempo.
- Encontre a velocidade máxima.
- Que aumento percentual seria obtido na velocidade máxima pela redução de em ?
Passo 1
Considerações Iniciais:
- Escoamento em estado estacionário;
- Escoamento incompressível;
- Escoamento com velocidade constante;
- Escoamento uniforme.
Passo 2
Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:
Como estamos analisando um sistema , temos:
Não há força de campo, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Então, :
Passo 3
Como e :
Assim:
Integrando:
Rearranjando:
Passo 4
Letra b)
A velocidade máxima é obtida quando o combustível é completamente queimado:
Agora, apenas substituiremos os dados na equação do Passo 3:
;
;
;
;
Então:
Passo 5
Letra c)
Sendo:
;
;
;
;
;
Então:
O aumento percentual é dado:
Passo 6
Letra a)
Para , considerar a equação:
Para :
Assim, com

Resposta
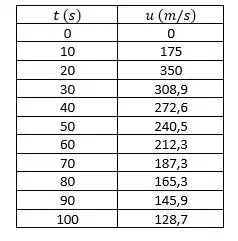
a) Gráfico
b)
c)