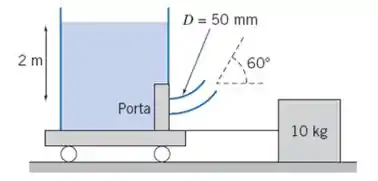
Um tanque de água está apoiado dobre um carrinho com rodas sem atrito como mostrado. O carro está ligado a uma por meio de um cabo e coeficiente de atrito estático da massa com o solo é . Se a porta bloqueando a saída do tanque é removida, o escoamento resultante na saída será suficiente para iniciar o movimento do tanque? (Considere que escoamento de água sem atrito, e que a velocidade do jato é , em que é a profundidade da água). Encontre o valor da massa justamente necessariamente para manter o tanque no lugar.

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

Como estamos analisando um sistema , temos:

Não há força de campo atuando, então, :

Não temos a variação das propriedades com o tempo, então:

Assim:

Sendo , temos:

;

.

A tração é dada por:

Sendo:

;

;

;

;

;

Temos:

Calculando a força de atrito máxima:

Sendo:

;

.

Temos:

A tensão criada pelo jato de água é menor que o atrito máximo, desse modo o tanque permanecerá em repouso.

Calculando a massa necessária para manter o tanque no lugar.

Temos que igualar a tração à força de atrito: