Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 115
Água é descarregada para a atmosfera a partir de um grande tanque, em regime permanente e através de um trecho de tubo de plástico liso. O diâmetro interno do tubo é 3,18 mm e seu comprimento é 15,3 m. Calcule a máxima vazão volumétrica para a qual o escoamento no tubo ainda será laminar. Estime o nível de água no tanque abaixo do qual o escoamento será laminar (para escoamento laminar, e 4).
Passo 1
Neste problema é pedido a máxima vazão volumétrica para que o escoamento no tubo ainda seja laminar. Também é pedido o nível de água a partir do qual o escoamento será laminar.
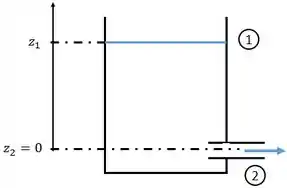
Será utilizada a Equação da Energia na forma:
Como hipótese e dados do enunciado tem-se que;
- regime permanente ();
- tubo horizontal;
- escoamento incompressível ();
- ;
- ;
- ;
- ;
- (pressão atmosférica em termos manométrico);
- (reservatório de grandes dimensões);
- ;
- perda por atrito dada por:
Passo 2
Para o escoamento ser laminar o número de Reynolds deve ser:
Isolando o termo :
Logo, a máxima velocidade para que o escoamento seja laminar é:
Sabendo que , então:
A velocidade máxima será de:
Passo 3
A vazão máxima pode ser definida como:
Utilizando os parâmetros conhecidos:
A vazão máxima vale:
Passo 4
Aplicando a Equação da energia entre as seções 1 e 2:
Sabendo que , , e conhecendo a expressão de ;
Logo, a altura de fluido no tanque é expressa por:
Como é pedido para avaliar a altura na situação de escoamento laminar é possível escrever o fator de atrito da seguinte forma:
Então, a altura pode ser escrita como:
Substituindo a expressão de por valores numéricos conhecidos e sabendo que a avaliação do escoamento se dá na faixa laminar:
Finalmente, conclui-se que o nível abaixo do qual o escoamento será laminar é: