Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 116

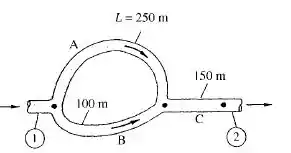
Para o sistema série-paralelo da figura a seguir, todos os tubos são de ferro fundido asfaltado de 8 cm de diâmetro. Se a queda total de pressão p 1 - p 2 = 750   k P a , determine a vazão resultante Q em m³/h para água a 20°C. Despreza as perdas localizadas.

Passo 1

Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!

Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.

ρ = 998   k g / m ³

μ = 0,001   k g / m . s

Bem, os tubos são feitos de ferro fundido asfaltado, ou seja, todos eles devem possuir a mesma rugosidade ϵ = 0 , 12   m m , portanto a rugosidade relativa é:

ϵ a = 0 , 12   x 10 - 3 8   x   10 - 2 = 0,00 15

Passo 2

A perda de carga é igual em qualquer que seja o caminho que o fluido percorrer, ou seja, AC e BC devem ter mesma perda de carga.

Δ p ρ g = h f A + h f C = h f B + h f C  

Δ p ρ g = f L D V 2 2 g A + f L D V 2 2 g C = f L D V 2 2 g B + f L D V 2 2 g C

Passo 3

Desde que os diâmetros dos tubos sejam iguais, vamos ter também que suas velocidades serão iguais e por balanço de massa, obtemos que:

V A + V B = V C

Podemos cancelar a gravidade na nossa fórmula do passo anterior,

Δ p ρ = f L D V 2 2 A + f L D V 2 2 C = f L D V 2 2 B + f L D V 2 2 C

Vamos precisar mais uma vez chutar f e vamos chutar 0,022.

Com isso teremos dois conjuntos de equação:

750000 998 = f 250 0,08 V 2 2 A + f 150 0,08 V 2 2 C = f 100 0,08 V 2 2 B + f 150 0,08 V 2 2 C

V A + V B = V C

Ao se chutar f = 0,022 e resolvermos o sistema acima, temos que

V A = 2,1   m / s

V B = 3,31   m / s

V c = 5,4   m / s

Passo 4

Vamos ter que iterar, porque agora com esses novos valores de velocidade, podemos calcular o Reynold e assim encontrar novos valores no diagrama de Moody dos fatores de atrito.

R e A = 167000 ,   f A = 0,023

R e B = 264000 ,   f B = 0,0226

R e c = 431000 , f C = 0,022

Entramos com esses novos valores de fator de atrito na equação do passo 3, encontramos novas velocidades, que por sua vez farão calcular novos Re e assim, voltamos achar um novo valor de fator de atrito. Note que esse processo deve ser feito até convergência.

Após convergência, você verá que os valores são:

V A = 2 , 06   m / s

V B = 3 , 29   m / s

V c = 5 , 35   m /

Portanto, a vazão é dada por:

Q = π 4 D 2 V c = π 4 0,08 2 5,35 = 0,0269   m 3 / s

Resposta

Q = 0,0269   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo que transporta óleo a 40 ° C a uma taxa de 3 m 3 s , se divide em dois tubos paralelos feitos de aço comercial que se reconectam a jusante. O tubo A tem 500m de comprimento e diâmetro de 30c m
Um tubo circular de água tem uma expansão abrupta do diâmetro D 1 = 15c m para D 2 = 20c m . A pressão e a velocidade média da água no tubo menor são P 1 = 120k P a e 10m / s , respectivamente, e o es
Em uma usina hidrelétrica a água a 20 ° C é fornecida para a turbina a uma taxa de 0,8m 3 / s através de um tubo de ferro fundido com 200m de comprimento e 0,35m de diâmetro. A diferença de elevação e
No Problema 8 - 112 , o diâmetro do tubo é triplicado para reduzir as perdas do tubo. Determine o aumento percentual na saída de potência liquida como resultado dessa modificação.
A água em uma piscina acima do solo a 20 ° C , com 10m de diâmetro e 2m de altura deve ser esvaziada destampando um tubo plástico horizontal com 3c m de diâmetro e 25m de comprimento anexado à parte i