Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 36

Água escoa através de um canal hexagonal com largura do fundo de 2   m a uma vazão de 45   m 3 / s . Determine (a) a velocidade média e (b) se o escoamento é subcrítico e super crítico.

Passo 1

Nessa questão nós temos que a água flui uniformemente através de um canal hexagonal meio cheio. Com isso, vamos calcular a velocidade média e se a vazão é subcrítica ou supercrítica a uma dada vazão.

Passo 2

A área de fluxo é determinada a partir de considerações geométricas indicadas abaixo,

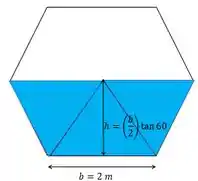
Onde,

A c = b + 2 b b 2 b 2 tan ⁡ 60 ° = 2 + 2 × 2 m 2 2 m 2 tan ⁡ 60 ° = 5,196 m 2

Então a velocidade média é,

V = V ˙ A c = 45 m 3 s 5,196 m 2 = 8,66 m / s  

Passo 3

Ao calcular o número de Froude, a profundidade hidráulica deve ser usada em vez da profundidade máxima ou do raio hidráulico.

Para um canal não retangular, a profundidade hidráulica é definida como a razão entre a área de fluxo e a largura superior,

y = y h = A c l a r g u r a   s u p e r i o r = A c 2 b = 5,196 m 2 2 × 2 m = 1,299 m

Então o número de Froude é,

F r = V g y = 8,66 m / s   ( 9,81   m / s 2 ) ( 1,299 m ) = 2,43

Que é maior que 1 . Portanto, o fluxo é supercrítico.

Resposta

  1. V = 8,66 m / s  
  2. F r = 2,43
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 13-53 para um canal de terra escavado coberto de vegetação com n =0,030 .
Reconsidere o Problema 13-50. Se a altura máxima de escoamento que o canal consegue acomodar é 2,4m , determine a vazão máxima de escoamento através do canal.
Considere o escoamento de água através de dois canais 13-52 idênticos com seções de escoamento quadradas de 3mx3m . Agora os dois canais são combinados, formando um canal com 6m de largura. A vazão é
Um canal trapezoidal com uma largura do fundo de 5m , largura de superfície livre de 10m , e profundidade de escoamento de 2,2m descarrega água a uma vazão de 120m 3 / s . Se as superficies do canal e
Água deve ser transportada em um canal aberto, cujas superfícies são revestidas com asfalto, uma taxa de 4m 3 / s no escoamento uniforme. A inclinacão inferior é 0,0015 . Determine as dimensões da mel