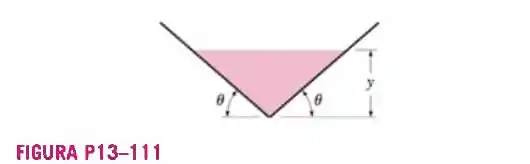
Considere o escoamento de água através de um canal em forma de V. Determine o ângulo que o canal faz com a horizontal para o qual o escoamento é mais eficiente.
Passo 1
Bora pra mais uma questão!!
Queremos dimensionar um canal triangular que tenha um escoamento mais eficiente possível. Para isso temos que descobrir quem é !
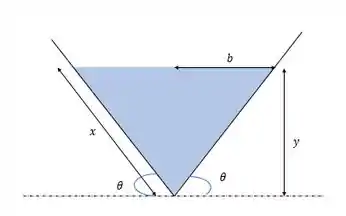
Em um canal aberto a melhor secção transversal é a que tem o menor perímetro possível para determinada área. E se a gente quer encontrar o mínimo o que a gente faz?!
Muito bem, a gente deriva e iguala a zero!!
Passo 2
Mas primeiro temos que descobrir uma equação para o perímetro em função de , sabendo que:
Sabendo que:
Então:
Mas a gente também não conhece temos que escrever ele em função de , então talvez esse não seja o caminho...
Vamos escrever tudo que a gente puder sobre as dimensões do canal pra ver onde a gente pode chegar:
A área transversal é dada por:
Opaa, apareceu o e o , então podemos substituir:
Usando a identidade trigonométrica,
Isolando o :
Agora substituindo na equação do perímetro:
Passo 3
Conseguimos escrever em função de , mas não do jeito que queriamos..ao invés do sozinho temos !
Mas calma, podemos dar um jeito nisso!
O que temos até agora é:
Podemos jogar pra fora quem é constante e reescrever de uma maneira mais interessante:
Passo 4
Opaa, e como a gente pode resolver essa derivada:
Vamos usar a regra da cadeia!!
Fazendo:
Mas para acharmos temos que usar regra da cadeia de novo, tipo no fime A Origem mesmo ahaha
Nesse caso fazemos:
Então:
Aplicando a regra da cadeia:
Substituindo:
Passo 5
Voltando para a regra da cadeia inicial:
Aplicando a regra da cadeia:
Derivando e substituindo :
Substituindo :
Arrumando:
Passo 6
Agora que derivamos, podemos voltar para essa expressão aqui:
Substituindo a derivada:
Queremos que essa derivada seja igual a zero, para isso precisamos de um que faça isso por a gente!
Sabendo que , então podemos fazer:
Opaaa, é isso mesmo?! Achamos nosso que vai fazer o escoamento ficar mais eficiente!!!
Uhuuul!!!