Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 50
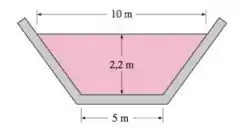
Um canal trapezoidal com uma largura do fundo de , largura de superfície livre de , e profundidade de escoamento de descarrega água a uma vazão de Se as superficies do canal estiverem revestidas com asfalto , determine a queda de elevação do canal por .
Passo 1
Nessa questão nós temos que a água deve ser transportada uniformemente em um canal revestido de asfalto trapezoidal. Para uma vazão especificada, a queda de elevação necessária por de comprimento de canal deve ser encontrada.
Passo 2
Para resolver essa questão vamos assumir:
- O fluxo é constante e uniforme;
- A inclinação inferior é constante;
- O coeficiente de rugosidade é constante ao longo do canal.
A área de fluxo, o perímetro úmido e o raio hidráulico do canal são,
Passo 3
Substituindo as quantidades dadas na equação de Manning,
Portanto, a queda de elevação em um comprimento de tubo de deve ser,
Resposta
Exercícios de Livros Relacionados
13-14 Água a 20®C escoa de modo uniforme em um canal largo e retangular a uma velocidade de 2 m/s. Se a profundidade da água for 0,2 m, determine (a) se o escoamento é laminar outurbulento e (b) se o
Considere o escoamento da água em um canal largo. Determine a velocidade de um pequeno distúrbio no escoamento se a profundidade de escoamento for (a) 10 cm e (è) 80 cm. Qualseria sua resposta se o fl
13-21C Considere o escoamento permanente da água através de dois canais retangulares abertos idênticos, com vazões idênticas. Se o escoamento em um canal é subcrítico e no outro é supercrítico, é poss
13-15 Água a 20°C escoa em um canal circular parcialmente cheio de 2 m de diâmetro a uma velocidade média de 2 m/s. Se a profundidade máxima da água for 0,5 m, determine o raiohidráulico, o número de
12-143 Ar de uma sala a T 0=300K e P 0 = 100k P a é retirado de forma constante por uma bomba a vácuo através de um tubo adiabático com 3 cm de diâmetro, 2 m de comprimento eum bocal convergente na en