Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 103

Um canal trapezoidal com largura inferior de 4 m e inclinação lateral de 45° descarrega água a uma vazão de 18 m³/s. Se a profundidade do escoamento for 0,6 m, determine se o

escoamento é subcrítico ou supercrítico.

Passo 1

Opaa, vamos começar desenhando um esqueminha??!!

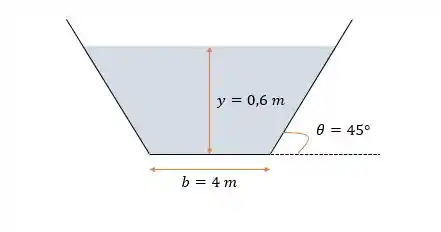
A gente quer conhecer o comportamento do escoamento, para isso usamos o número de Froude:

F r = V g y h

Mas não conhecemos a velocidade e esse y h que aparece aqui é diferente do y dado no problema, ele é a profundidade hidráulica!

Temos que ir atrás desses carinhas!!

Passo 2

Começando pela velocidade:

V = V ˙ / A c

Para calcular A c de um canal trapezoidal fazemos:

A c = b + y tan ⁡ θ y    

Substituindo:

A c = 4 + 0,6 tan ⁡ 45 ° 0,6 = 2,76   m 2    

Agora podemos calcular a velocidade:

V = 18 2,76 = 6,522   m / s

Passo 3

Agora vamos calcular a altura hidráulica, y h :

y h = A c Á r e a   s u p e r i o r   = A c b + 2 y tan ⁡ θ

Substituindo:

y h = 2,76 4 + 2 × 0,6 tan ⁡ 45 °

Calculando:

y h = 0,5308   m

Passo 4

Finalmente podemos calcular o número de Froude:

F r = 6,522 9,81 × 0,5308 = 2,86

Se F r > 1 , então o escoamento é supercrítico!!

Resposta

O escoamento é supercrítico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-101 Repita o Problema 13-100 para uma profundidade de escoamento a montante de 2,2 m.
Um canal de drenagem de aço circular com 2 m de diâmetro interno (n = 0,012) deve descarregar água de modo uniforme a uma vazão de 12 m³/s até uma distância de 1 km. Sea profundidade máxima deve ser 1
Água escoa através de um canal retangular com 1,5 m de largura com um coeficiente de Manning de n = 0,012. Se a profundidade da água for 0,9 m e a inclinação do fundo do canalfor 0,6°, determine a tax
Um reservatório triangular com soleira espessa e ângulo de entalhe de 100° é usado para medir a taxa de descarga da água de um lago grande para um escoadouro. Se, em vez disso, for usado um reservatór
Um canal retangular com largura do fundo de 2 m descarrega água a uma vazão de 8 m³/s. Determine a profundidade de escoamento abaixo da qual o escoamento é supercrítico.