Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 201
Líquido, em um jato fino de largura e espessura , escoa de uma ranhura e atinge uma placa plana estacionária. Experiências mostram que a força resultante do jato de líquido sobre a placa não atua através do ponto , em que a linha de centro do jato intercepta a placa. Determine o módulo e a linha de ação da força resultante como funções de . Avalie o ângulo de equilíbrio da placa, se a força resultante fosse aplicada no ponto . Despreze qualquer efeito viscoso.
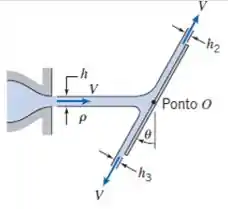
Passo 1
Equações:
Considerações Iniciais:
- Fluxo Constante;
- Escoamento Estacionário;
- Cancelamento do torque no corpo;
- Sem Efeitos de Viscosidade .
- .
Realizando as considerações, temos respectivamente:
Passo 2
Da equação da continuidade, temos:
Simplificando:
Da equação de momento:
Sendo:
;
;
.
Temos:
Passo 3
Combinando as duas equações obtidas no Passo 2, temos:
e
Do momento , temos:
Sendo:
;
;
.
Temos:
Passo 4
Aplique a equação de momento do momento da seguinte forma:
Sendo:
;
;
;
;
;
/
;
;
;
Substituindo na equação do momento do momento, temos:
Isolando :
Passo 5
Utilizando as relações obtidas no Passo 3, e substituindo :
Passo 6
Observe que , isso significa que deve ser aplicado abaixo do ponto 0.
Se é aplicado no ponto 0, , para o equilíbrio, a partir da equação obtida, . Assim, se a força for aplicada no ponto 0, a placa estará em equilíbrio quando perpendicular ao jato.