Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 188

Um regador comum de gramados pode girar no plano horizontal, conforme mostrado. Água entra verticalmente pelo pivô central com uma vazão Q = 15   L / m i n . A água é descarregada em jatos através dos dois bicos no plano horizontal. Considerando o pivô sem atrito, calcule o torque resistente necessário para manter o regador imóvel. Desprezando a inércia do regador, calcule a aceleração angular que resulta quando o torque resistente é removido.

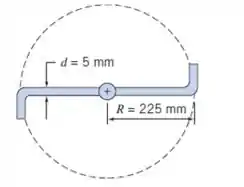
Passo 1

Equação

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Uniforme;
  3. Escoamento Estacionário;
  4. Sem Atrito;

Passo 2

Realizando as considerações apresentadas no Passo 1, temos:

∫ V C r × g ρ d ∀ + T e i x o = ∫ S C r × V   ρ V d A

Substituindo r × g = r × r × α = r 2 α :

∫ V C r 2 α ρ d ∀ + T e i x o = ∫ S C r × V   ρ V d A

Integrando:

T e i x o + α d 2 ρ R 3 π 12 = R V ρ Q 2  

Passo 3

Quando α = 0 :

T e i x o = R V ρ Q 2

Sendo:

R = 225   m m = 0,225   m ;

Q = 15   L / m i n = 0,00025 m 3 / s ;

A = π d 2 4 = π 0,005 2 4 = 1,96 x 10 - 5   m 2 ;

ρ = 1000   k g / m 3 ;

V = Q 2 A = 6,37   m / s .

Temos:

T e i x o = 0,225 ⋅ 6,37 ⋅ 1000 ⋅ 0,00025 2 = 0,179   N ⋅ m

Como o torque total é a soma dos dois eixos, temos:

T t o t a l = 2 ⋅ 0,179 = 0,358   N ⋅ m

Passo 4

Desprezando a inércia do regador, calcule a aceleração angular que resulta quando o torque resistente é removido.

T e i x o = 0

Então:

α = 6 V Q d 2 R 2 π

Substituindo os dados:

α = 6 ⋅ 6,37 ⋅ 0,00025 ( 0,005 ) 2 ⋅ 0,225 2 π = 2403   s - 2

Resposta

T t o t a l = 0,358   N ⋅ m

α = 2403   s - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A junta em Y da Figura P3.112 divide a vazão no tubo em partes iguais Q/2, que saem à distância R 0 do eixo, como mostra a figura. Despreze a gravidade e o atrito. Encontre uma expressão para o torque
Um foguete é ligado a uma barra rígida horizontal, articulada na origem, como na Figura P3.104. Sua massa inicial é M 0 e suas propriedades de saída são m ˙ e V s , relativas ao foguete. Estabeleça a
Estenda o Problema P3.104 para o caso em que o foguete sofre uma força de arrasto do ar, F = c V , em que c é uma constante. Considerando que o combustível não acaba, determine ω ( t ) e encontre a ve
Admita que o foguete com propelente sólido do problema P3.35 seja instalado em um míssil de 70 cm de diâmetro e 4 m de comprimento. O sistema pesa 1800 N, incluindo 700 N de propelente. Despreze o arr
Reverta o escoamento na Figura P3.116, de modo que o sistema passe a operar como uma turbina de fluxo radial. Considerando que o escoamento na seção de saída 1 não tem velocidade tangencial, deduza um