Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 196

No Problema 4.195, calcule a aceleração inicial do regador a partir do repouso, considerando que não haja torque externo aplicado e que o momento de inércia do cabeçote de irrigação é de 0,1   k g ⋅ m 2 quando cheio de água.

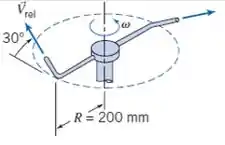
Passo 1

Equação:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Estacionário;
  3. Cancelamento do torque no corpo;
  4. F S = 0 .

Passo 2

Realizando as considerações:

T e i x o = ∫ S C r × V   ρ V d A

Temos:

T e i x o = - T f k ^

- T f k ^ = r × V m - ρ Q + 2 r × V j a t o ρ Q 2

Sendo:

r × V m = 0 ;

r = R   î r ;

V = R ω - V r e l cos ⁡ α î θ + V r e l   s e n   α   î z .

A velocidade absoluta do jato de saída é:

V = V r e l cos ⁡ α - î θ + s e n   α   î z

r × V = R   î r × V r e l cos ⁡ α - î θ + s e n   α   î z

Sendo:

î r × î θ = î z ;

î r × î z = - î θ ;

Temos:

r × V = R V r e l cos ⁡ α - î z + s e n   α   - î θ

Então:

r × V z = - R V r e l cos ⁡ α

Desse modo:

- T f = 2 - R V r e l cos ⁡ α ⋅ ρ Q 2

T f = R V r e l ρ Q cos ⁡ α

∑ T = R V r e l ρ Q cos ⁡ α - T f

Pela condição de equilíbrio dos momentos:

∑ M = I ω

Então:

∑ T = I ω

Isolando ω :

ω = ∑ T I = R V r e l ρ Q cos ⁡ α - T f I

Passo 3

Sendo:

T f = 0,18   N ⋅ m ;

R = 200   m m = 0,2   m ;

V r e l = 17   m / s ;

ρ = 1000   k g / m 3 ;

Q = 4   L / m i n = 6,67 x 10 - 5   m 3 / s ;

θ = 30 ° ;

I = 0,1   N ⋅ m .

Temos:

ω = 0,2 ⋅ 17 ⋅ 1000 ⋅ 6,67 x 10 - 5 ⋅ cos ⁡ 30 ° - 0,18 0,1 = 0,164   r a d / s 2

Resposta

ω = 0,164   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Retome a grade de turbina do Problema P3.78 e deduza uma fórmula para a potência P desenvolvida, usando o teorema da quantidade de movimento angular da Equação (3.55).
O irrigador de gramados horizontal da Figura P3.110 tem uma vazão d’água de 15,2 L/min, introduzida verticalmente pelo centro. Calcule (a) o torque resistente necessário para manter os braços sem rota
Admita que o foguete com propelente sólido do problema P3.35 seja montado em um carro de 1000 kg para propulsioná-lo por um longo aclive de 15°. O motor de foguete pesa 900 N, incluindo 500 N de prope
Água a 20°C escoa a 114 L/min através do tubo de 19 mm de diâmetro com duas curvas, como na Figura P3.115. As pressões são p 1 = 206,84k P aep 2 = 165,47k P a . Calcule o torque T no ponto B necessári
Como se pode observar frequentemente em uma pia de cozinha quando a torneira está aberta, um escoamento com alta velocidade em um canal ( V 1 , h 1 ) pode “saltar” para uma condição de baixa velocidad