Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 72
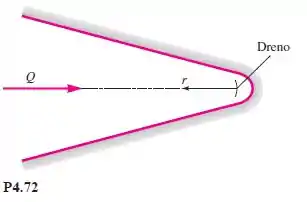
A água escoa por um canal bidimensional com estreitamento em forma de cunha a 0,63 L/s por metro de largura na direção perpendicular ao papel (Figura P4.72). Se esse escoamento para dentro é puramente radial, encontre uma expressão para (a) a função corrente e (b) o
potencial de velocidade do escoamento. Considere escoamento unidimensional. O ângulo formado pela cunha é de 45.
Passo 1
Bora pra mais uma!
- Sendo 45 = radianos, em qualquer posição o fluxo interno será igual a:
Onde é a área do escoamento, daí:
Note que o valor do raio deverá ser em metros.
Como enunciado, o escoamento é puramente radial, ou seja, , daí a função corrente é:
Sendo r em metros.
Resposta
A função corrente e o potencial de velocidade são respectivamente:
Com o valor de r em metros.
Exercícios de Livros Relacionados
Considere o ar escoando sobre um hemisfério assentado sobre uma superfície plana, como na figura a seguir. Se a pressão interna é p i , encontre uma expressão para a força de pressão sobre o hemisféri
Se ϕ ( r , θ ) no escoamento com simetria axial é definida pela equação 8.85 e as coordenadas são dadas na figura 8.29, determine qual a equação diferencial parcial que ϕ deve satisfazer.
Mostre que o escoamento potencial com simetria axial formado pela superposição de uma fonte pontual + m em x , y = ( - a , 0 ) , um sumidouro pontual - m em ( + a , 0 ) e uma corrente U ∞ na direção x
Um semicorpo de Rankine de revolução (Figura 8.31) pode simular o formato de um tubo de Pitot estático (figura 6.30). Segundo a teoria não viscosa, a que distância a jusante do nariz deveria ser posic
Suponha que uma esfera com um orifício de estagnação simples é usada como velocímetro. A pressão nesse orifício é usada para calcular a velocidade U da corrente, mas há erros se a corrente não estiver