Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 99
Considere o ar escoando sobre um hemisfério assentado sobre uma superfície plana, como na figura a seguir. Se a pressão interna é , encontre uma expressão para a força de pressão sobre o hemisfério. Por analogia com o problema 8.49, em que ponto A sobre o hemisfério se deve perfurar um orifício de modo que a força de pressão seja zero segundo a teoria não viscosa?
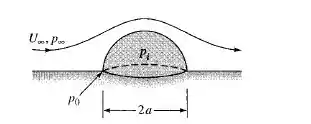
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!
Vamos chamar a equação 8.100 que diz que a velocidade ao longo de uma superfície esférica pode ser dada por:
Além disso o livro também nos diz que a força que atua na parte superior pode ser dada pela seguinte equação abaixo.
Passo 2
Mas quem é essa pressão de superfície? É o que chamamos de pressão de Bernoulli, que também temos a equação prontinha já no livro!!!
Resolvendo nossa equação da força ali do passo 1, já substituindo , a gente vai ter a força com essa carinha aí embaixo ó:
Passo 3
A força deve ser igual a ZERO se nos colocarmos um orifício ali no ponto A , tal que:
Onde o subíndice “i” indica o nosso ponto de interesse de estudo, ou seja, o nosso ponto A!!
Ou melhorando isso aí que escrevemos, podemos ter que
Resolvendo nossa igualdade temos que ouuuuu 135°