Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 95

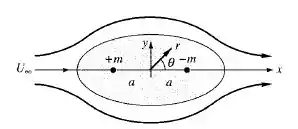
Mostre que o escoamento potencial com simetria axial formado pela superposição de uma fonte pontual + m em x , y = ( - a , 0 ) , um sumidouro pontual - m em ( + a , 0 ) e uma corrente U ∞ na direção x forma um corpo de revolução de Rankine, como na figura abaixo. Encontre expressões analíticas para determinar o comprimento 2L e o máximo diâmetro 2R do corpo em termos de m ,   U ∞ e a .

Passo 1

As funções de linhas de corrente para essa física são dadas abaixo, e o formato do corpo (revolução de Rankine) é dado por ψ = 0

ψ = - U 2 r 2 s e n 2 θ + m c o s θ 2 - c o s θ 1

Passo 2

Os pontos de estagnação em r = L, θ = 0 ,   π ou U + m L + a 2 - m L - a 2 = 0

Resolvendo isso para deixarmos do jeito que é pedido:

L a 2 - 1 2 = 4 m U a 2 L a

Passo 3

Similarmente para o raio máximo R nesse formato oval que temos aí em cima, ocorrerá qiando ψ = 0 e θ = ± 90 °

0 = - U 2 R 2 + 2 m c o s θ 2

Onde c o s θ 2 = a a 2 + R 2

De forma a ficar melhor escrito, temos que:

R a 2 1 + R a 2 = 4 m U a 2

Resposta

L a 2 - 1 2 = 4 m U a 2 L a

R a 2 1 + R a 2 = 4 m U a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.28 A função de corrente para certo ampo de escoamento incompressível é dada pela expressão ψ = - U rs e nθ + q θ / 2 π . Obtenha uma expressão para o campo de velocidade. Encontre o(s) ponto(s) de e
5.25 Exemplo 5.7 é V → = U ( y / h ) î î. Dermine a função de corrente para este escoamento. Localize a linha de corrente que divide a vazão volumétrica total em duas partes iguais.
Sources of strength m 5 10 m2/s are placed at points A andB in Fig. P8.23. At what height h should source B be placedso that the net induced horizontal velocity component atthe origin is 8 m/s to the
A large Rankine oval, with a 5 1 m and h 5 1 m, isimmersed in 208C water fl owing at 10 m/s. The upstreampressure on the oval centerline is 200 kPa. Calculate (a) thevalue of m; and (b) the pressure o
Water at 208C fl ows past a 1-m-diameter circular cylinder.The upstream centerline pressure is 128,500 Pa. If the lowest pressure on the cylinder surface is exactly the vaporpressure, estimate, by pot