Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 54

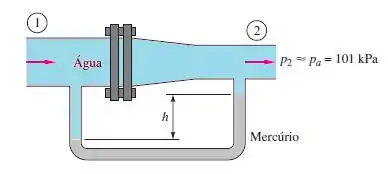
Para o escoamento na redução de seção do tubo da figura abaixo, com D 1 = 8   c m , D 2 = 5   c m e p 2 = 1   a t m . Todos os fluidos estão a 20°C. Se V 1 = 5   m / s e a leitura do manômetro é de h = 58   c m , calcule a força total à qual os parafusos dos flanges resistem.

Passo 1

E aí, galeraaa! Preparados? Se sim ou se não, vem comigo que vai ser sucesssooo!!!

Vamos fazer um volume de controle em volta dos flanges igual abaixo:

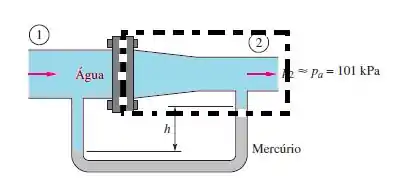
Vamos agora escrever o balanço de forças que atuam na direção X!!!

F P 1 + m ˙ e u e - F f l a n g e - F P 2 - m ˙ s u s = 0

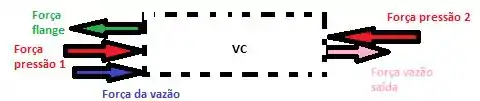
Sabemos que a força de pressão é dada pelo produto entre a área de atuação da força e o valor da pressão naquela área. Além disso, como observamos acima a área de atuação é igual para a pressão 2 e pressão 1, onde a pressão 2 é a atm.

Outra observação válida é que como estamos em uma física de fluido incompressível, a vazão de entrada deve ser igual a vazão de saída!!

A 1 p 1 - p a t m - F f l a n g e + m ˙ V 1 - V 2 = 0

Passo 2

Note que precisamos calcular os parâmetros do nosso balanço e o problema estará resolvido.

p 1 = ρ á g u a g h

p 2 = ρ H g g h

p 1 = p 2

p 1 - p 2 = ρ H g - ρ á g u a g h = 13280 - 979 10 0,58 = 71300   P a

Para encontrar o valor de V 2 , precisamos aplicar o balanço de massa, tal que:

Q 1 = Q 2 → V 1 π 4 D 1 2 = V 2 π 4 D 2 2

5 π 4 0,08 2 = V 2 π 4 0,05 2 → V 2 = 12,8   m / s

Passo 3

Agora vamos substituir os valores no nosso balanço de forças e ser feliz

A 1 p 1 - p a t m - F f l a n g e + m ˙ V 1 - V 2 = 0

π 4 D 1 2 p 1 - p a t m - F f l a n g e + ρ A 1 V 1 V 1 - V 2 = 0

π 4 0,08 2 71300 - F f l a n g e + 998 π 4 0,08 2 5 12,8 - 5 → F f l a n g e = 163   N

Resposta

F = 163   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jato d’água horizontal, com taxa de escoamento V ˙ e área de seção transversal A , movimenta um carrinho coberto de massa m c ao longo de uma trajetória nivelada e quase sem atrito. O jato entra em
Considere um avião com um motor a jato anexado à seção da cauda que expele gases de combustão a uma taxa de 18k g / s com velocidade de V = 250m / s com relação ao avião. Durante a aterrisagem, um rev
Um jato d’água horizontal com 5c m de diâmetro e velocidade de 30m / s atinge a ponta de um cone horizontal, o qual deflete a água a 45 ° de sua direção original. Qual a força necessária para manter o
A figura abaixo mostra um tripé segurando um bocal que direciona uma corrente de água com 5c m de diâmtro de uma mangueira. A massa do bocal é de 10k g quando está cheio com água. O tripé é classifica
Um soldado salta de um avião e abre o paraquedas quando sua velocidade atinge a velocidade terminal V t . O paraquedas diminui sua velocidade até a velocidade de aterrisagem de V f . Após o uso dele,