Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 104

Água escoa do tanque mostrado através de um tubo muito curto. Considere que o escoamento seja quase permanente. Estime a vazão no instante mostrado. Como você poderia melhorar o sistema de escoamento se uma vazão maior fosse desejada?

Passo 1

Neste problema é pedido a vazão que sai por um tubo curto no momento mostrado na Figura.

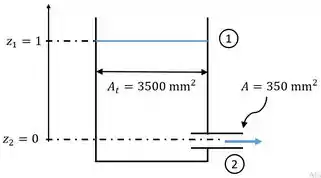
Será utilizada a Equação da energia na forma:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l T

Sendo a perda de carga total definida como:

h l T = f L D V 2 2   2   + K V 2 2 2

Como hipótese e dados do enunciado tem-se que;

- regime permanente ( ∂ / ∂ t = 0 );

- z 1 = 1   m ;

- z 2 = 0   m ;

- escoamento incompressível ( ρ 1 = ρ 2   e ρ á g u a = 1000   k g / m 3 );

- α ≈ 1,0 ;

- A 1 = 3500   m m 2 ;

- A 2 = 350   m m 2 ;

- L ≈ 0 (tubo de pequeno comprimento);

- p 1 = p 2 = 0 (pressão atmosférica em termos manométrico).

Passo 2

Usando a Equação de Energia, em J/kg, entre as seções 1 e 2:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l T

p 1 ρ - p 2 ρ = α V 2 2 2 - α V 1 2 2 + g ( z 2 - z 1 ) + h l T

p 1 - p 2 = ρ α V 2 2 - V 1 2 2 + ρ g z 2 - z 1 + ρ h l T

Sabendo a expressão de h l T , que z 2 = 0 , z 1 = h , α ≈ 1 e p 1 - p 2 :

0 = ρ V 2 2 - V 1 2 2 - ρ g h + ρ f L D V 2 2   2   + K V 2 2 2

Mas pela hipótese de comprimento do tubo curto:

ρ f L D V 2 2   2 ≈ 0

Então:

0 = ρ V 2 2 - V 1 2 2 - ρ g h + ρ K V 2 2 2

V 1 2 - V 2 2 2 + g h = K V 2 2 2

Passo 3

Escrevendo as velocidade em termo dos parâmetros dados no enunciado:

Q 1 = Q 2

V 1 A 1 = V 2 A 2

Logo:

V 1 = V 2 A 2 A 1

Passo 4

Então a expressão obtida no Passo 2 é escrita como:

V 2 A 2 A 1 2 - V 2 2 2 + g h = K V 2 2 2

V 2 2 2 A 2 A 1 - V 2 2 2 + g h = K V 2 2 2

g h = K V 2 2 2 - V 2 2 2 A 2 A 1 + V 2 2 2

g h = V 2 2 2 K + 1 - A 2 A 1 2

Então a velocidade pode ser escrita como:

V 2 2 = 2 g h K + 1 - A 2 A 1 2

V 2 = 2 g h K + 1 - A 2 A 1 2

Passo 5

A partir da Tabela 8.2 é definido, para tubo reentrante, o coeficiente de perda de carga:

K = 0,78

Passo 6

Calculando o valor de V 2 :

V 2 = 2 g h K + 1 - A 2 A 1 2

V 2 = 2 × 9,81 × 1 0,78 + 1 - 350 3500 2

Logo, a velocidade na seção 2 é de:

V 2 = 3,33   m / s

Passo 7

A vazão será dada por:

Q = V 2 A 2

Q = 3,33 × ( 350 × 10 - 6 )

Q = 1,17 × 10 - 3   m 3 / s

Ou ainda:

Q = 1,17   L / s

Passo 8

Para aumentar a velocidade será necessário alterar a velocidade V 2 , a qual tem a seguinte expressão:

V 2 = 2 g h K + 1 - A 2 A 1 2

Logo deve ser buscado a redução do coeficiente K , que pode ser feita pelo arredondamento da entrada do tubo ou ainda pela alteração do tubo para borda viva.

Resposta

Q = 1,17 × 10 - 3   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145
Dois tanques com água a 20°C são conectados por um tubo capilar de 4 mm de diâmetro e 3,5 m de comprimento. A superfície do tanque 1 está 30 cm acima da superfície do tanque 2. (a) Estime a vazão em m
Óleo SAE 10 a 20°C escoa em um tubo vertical de 2,5 cm de diâmetro. Verifica-se que a pressão é constante em todo o fluido. Qual é a vazão de óleo em m³/h? O escoamento é para cima ou para baixo?
Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então cor
A fim de determinar a viscosidade de um líquido de densidade de 0,95, você preenche, a uma profundidade de 12 cm, um grande recipiente com drenagem por um tubo vertical de 30 cm de comprimento fixado