Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 20

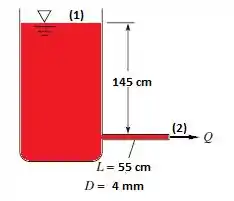
Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145 cm abaixo da superfície do tanque. O fluido é óleo combustível médio, ρ = 850   k g / m ³ e μ = 0,11   k g / ( m . s ) . Estime a vazão de óleo em cm³/h.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Vamos agora escrever nossa equação de energia nos dois pontos que estão na figura!!

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h f

Passo 2

Vamos para nossas hipóteses para simplificar nossa equação!

p 1 = p 2 = p a t m

V 1 = 0

Então nossa equação fica da seguinte forma:

z 1 - z 2 = V 2 2 2 g + h f

Passo 3

Bem, vamos supor inicialmente que estamos em regime laminar, beleza? Isso vai facilitar nossas contas para termos uma suposição inicial!!!

Para escoamento laminar, temos que:

h f = 32 μ L V ρ g d 2

z 1 - z 2 = V 2 2 2 g + h f

Δ z - V 2 2 2 g = h f = 32 μ L V ρ g d 2

Note que V 2 = V , pois a velocidade do fluido dentro do tanque V , deve ser igual a velocidade do fluido no ponto 2, que é a iminência de sua saída de dentro do tubo, beleza?

Δ z - V 2 2 g = 32 μ L V ρ g d 2

Temos uma equação quadrática em V, onde apenas a raiz positiva é o que tem sentido físico para gente, certo?

1,45 - V 2 19,62 = 32 0,11 0,55 V 850 9,81 0,004 2 = 14,5 V

V 2 19,62 + 14,5 V - 1,45 = 0

V 2 + 284,5 V - 28,5 = 0

V = - b + b 2 - 4 a c 2 a = - 284,5 + 284,5 2 - 4 - 28,5 2 = - 284,5 + 284,7 2 = 0,1   m / s

Passo 4

Ou seja, nossa vazão supondo escoamento laminar é dada por:

Q = A V = π 4 d 2 V = π 4 0,004 2 0,1 = 1,256   x   10 - 6 m 3 s = 1,256   c m 3 / s

Vamos checar nosso valor de Reynold, porque se for laminar, já encontramos nossa vazão!!!

R e = ρ V d μ = 850 0,1 0,004 0,11 = 3,1   ( L a m i n a r )

Resposta

Q = 1,256   c m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em 1930, Theodore von Kármán propôs que o cisalhamento turbulento poderia ser representado por τ t u r b = ϵd u / d y , em que ϵ = ρ k 2 y 2| d u / d y | é denominada viscosidade turbulenta de comprim
Por analogia com a Equação (6.21), escreva a equação diferencial da quantidade de movimento turbulenta média para (a) a direção y e (b) a direção z. Quantos termos de tensão turbulenta aparecem em cad
Admita na Figura P6.37 que h = 3c m , o fluido é água a 20°C e o escoamento é turbulento, de tal modo que a lei logarítmica seja válida. Se a tensão de cisalhamento no fluido é 15 Pa, qual é V em m/s?
Dois reservatórios, com diferença de elevação de 40 m entre suas superfícies, estão conectados por um tubo novo de 8 cm de diâmetro e 350 m de comprimento. Se a vazão desejada for de, pelo menos, 500
Por analogia com o cisalhamento laminar, τ = μd u / d y , T. V. Boussinesq postulou, em 1877, que o cisalhamento turbulento poderia também ser relacionado com o gradiente de velocidade média τ t u r b