Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 69

Uma placa retangular uniforme, com 40 cm de comprimento e 30 cm de profundidade na direção normal ao papel, está suspensa no ar através de uma dobradiça na sua parte superior (no lado de 30 cm). Ela é atingida no centro por um jato horizontal de 3 cm de água movendo-se a 8 m/s. Se a comporta tiver uma massa de 16 kg, calcule o ângulo que a placa fará com a vertical.

Passo 1

Primeiro de tudo vamos idealizar nosso desenho e já colocar as forças que estão atuando sobre essa nossa placa retangular, beleza?

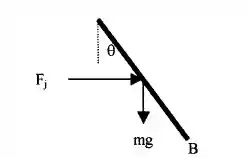
Passo 2

Po, aqui se a gente quer calcular o ângulo de alguma coisa nesse tipo de exercício, provavelmente isso virá do balanço de forças. Então vamos fazer nosso balanço de forças na direção x pra ver o que encontramos!!!

∑ F x = F j = - m ˙ e V j = - ρ A j V j V j = - ρ A j V j 2

Mas quem é essa área do jato? Isso é a área quem tem a seção transversal do jato, ou seja, π 4 0,03 2 , pois o jato tem 3 cm como dito no enunciado.

F j = - 998 π 4 0,03 2 8 2 = - 45,1   N

Passo 3

Beleza, mas até então não apareceu nosso ângulo pra podermos calcular ele! Então vamos aplicar agora o balanço de momento em torno do ponto B, beleza?

∑ M B = F j d j , B + W d W , B = 0

Onde o subíndice j,B indica que é a distância do jato até o ponto B. Enquanto o subíndice W,B significa a distância da força peso até o ponto B. A força peso nós assumimos que ela sempre atuará no centro da placa.

c o s θ = d W , B 0,02 → d W , B = 0,02   c o s θ

s e n θ = d j , B 0,02 → d j , B = 0,02   s e n θ

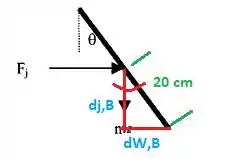
Passo 4

Substituindo dentro do nosso balanço, temos então que:

∑ M B = F j d j , B + W d W , B = F j d j , B + m g d W , B = 0

- 45 0,02 s e n θ + 16   x   10   x   0,02 c o s θ = 0

- 0,9   s e n θ + 3,2   c o s θ = 0

3,2   c o s θ = 0,9   s e n θ → s e n θ c o s θ = t a n θ = 3,2 0,9 = 3,55

θ = 16 °

Resposta

θ = 16 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa no duto abaixo que tem 50 cm de largura e 1 m de profundidade no sentido normal à página. A comporta BC fecha completamente o duto quando β = 90 ° . Considerando escoamento 1D, para qual ân
O tanque d’água abaixo situa-se sobre um carrinho sem atrito e alimenta um jato de 4 cm de diâmetro e 8 m/s de velocidade, que é defletido 60° por uma pá fixa. Calcule a tensão no cabo de suporte.
Um funil de carga descarrega cascalho à taxa de 650 N/s sobre uma correia transportadora como mostra abaixo. Em seguida o cascalho é transportado até o final da correia. As rodas de acionamento têm 80
Uma bomba dentro de um tanque de água a 20°C direciona um jato a 13,7 m/s e 757 L/min contra uma pá como mostrado abaixo. Calcule a força F para manter o carro parado se o jato segue (a) a trajetória
A draga da figura a seguir está carregando a barcaça com areia (d =2,6). A areia deixa o tubo da draga a 1,21 m/s com uma vazão em peso de 3781 N/s. Calcule a tensão no cabo de ancoragem causada por e