Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 37

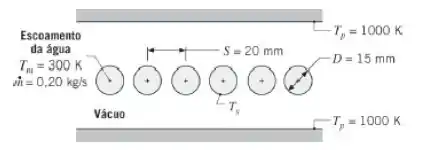
Água escoando através de um grande número de longos tubos circulares com paredes delgadas é aquecida por placas paralelas quentes, localizadas acima e abaixo da linha de tubos. Há vácuo no espaço entre as placas e as superfícies das placas e dos tubos podem ser aproximadas por corpos negros.

  1. Desprezando variações axiais, determine a temperatura na superfície do tubo, T s , se a água escoar através de cada tubo com uma vazão mássica de m ˙ =   0,20 k g s e a uma temperatura média T m =   300   K .
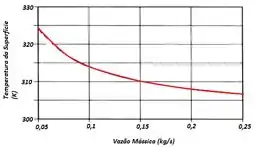
  2. Calcule e represente graficamente a temperatura superficial como uma função da vazão para 0,05   ≤   m ˙ ≤   0,25 k g s .

Passo 1

Vamos que vamos galerinha ?!

Bom, na letra (a) nós queremos achar a temperatura na superfície do tubo, T s , não é?

Para isso nós precisamos de fazer o balanço de energia para os tubos circulares, que estão recebendo calor por radiação e perdendo por convecção:

h A s T s - T m = A p F p s σ T p 4 - T s 4

Vamos ver o que temos?

σ = 5,67 × 10 - 8 W m 2 K 4

T p = 10 00   K

T m = 300   K

A s = π D = 0,015   m π = 0,0471   m

A p = 2 S = 2 0,02 = 0,04   m

m ˙ =   0,20 k g s

Então nós só não temos o coeficiente convectivo e o fator forma !!

Vamos começar com o coeficiente, e para isso nós precisamos do Reynolds:

R e D = 4 m ˙ π D μ

Para a água a 300 K nós podemos olhar na Tabela A – 6:

μ = 855 × 10 - 6 N s m 2

k = 0,613 W m K

P r = 5,83

Então:

R e D = 4 × 0,2 π 0,015 855 × 10 - 6 = 19855,6

Como o fluxo é turbulento nós podemos calcular o coeficiente convectivo como:

h = k D 0,023 R e D 4 5 P r 0,4

Substituindo:

h = 0,613 0,015 0,023 19855,6 4 5 5,83 0,4 = 5220 W m 2 K

Bom, nós ainda não temos os fatores de forma, não é?

Passo 2

Os fatores de forma são tabelados, não é? E neste caso podemos calcular F p s usando a fórmula:

F 13 = 1 - 1 - D s 2 1 2 + D s tan - 1 ⁡ s 2 - D 2 D 2 1 2

Onde D é o diâmetro e s o espaçamento:

D = 1 5   m m

s = 20   m m

Então:

F p s = 1 - 1 - 1 5 20 2 1 2 + 1 5 20 tan - 1 ⁡ 20 2 - 1 5 2 1 5 2 1 2 = 0 , 881

Substituindo:

5220 0,0471 T s - 300 = 0,04 0,881 5,67 × 10 - 8 1000 4 - T s 4

T 4 = 308   K

Finalizamos a letra (a), mas ainda não terminamos !!

Passo 3

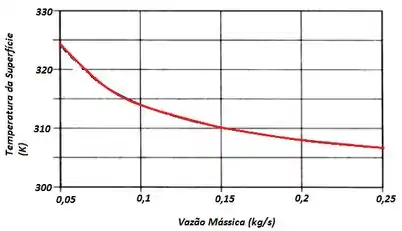
A letra (b) nos pede para representar graficamente a temperatura superficial como uma função da vazão para 0,05   ≤   m ˙ ≤   0,25 k g s .

Então nós faremos o Passo 1 e 2 novamente, somente variando a vazão mássica, e para isso vamos utilizar o software IHT:

Sucessooo galerinhaa, terminamos mais umaa !!

Resposta

  1. T 4 = 308   K
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um gás de exaustão, a uma pressão total de 1 atm e a temperatura de 1400 K, contém CO2 e vapor de água a pressões parciais de 0,05 e 0,10 atm, respectivamente. Se o gás escoa através de uma longa cham
Um forno é constituído por duas grandes placas paralelas que estão separadas entre si por uma distância de 0,75 m. Uma mistura gasosa composta por O2, N2, CO2 e vapor de água, com frações molares de 0
Em um processo industrial, produtos de combustão, a uma temperatura e pressão de 2000 K e 1 atm, respectivamente, escoam através de uma longa tubulação com 0,25 m de diâmetro, cuja superfície interna
Observando na Figura 13.16 que a emissividade de gases pode ser aumentada pela adição de vapor de água, é proposto aumentar a transferência de calor com a injeção de vapor de água saturado a 100°C na
A recuperação de calor dos gases de exaustão de um forno de fundição é feita com a passagem dos gases através de um tubo metálico vertical e a introdução de água saturada (estado líquido) na parte inf