Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 51

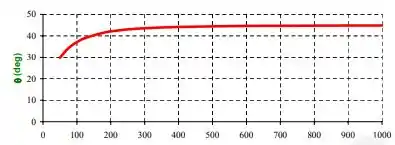
A altura de um edifício pode ser estimada em uma distância horizontal horizontal até um ponto no solo e o ângulo desse ponto ao topo do edifício. Supondo que essas medições sejam L   =   30   ±   0,15   m e θ   =   30   ±   0,2   ° , calcule a altura H do edifício e a incerteza na estimativa. Para a mesma altura de construção e as mesmas incertezas de uso, utilize o Excel planeado para determinar o ângulo (e a uma distância correspondente a partir do edifício) para qualificar como medições devem ser feitas para minimizar a incerteza na estimativa da altura. Avalie e trace um gráfico do ângulo de exibição ótimo como a função de altura do edifício para 15   ≤   H   ≤   300   m .

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, temos que:

L = 30 m

δ L = 0,15 m

θ = 30 º

δ θ = 0,2 º

A incerteza é dada por:

u L = δ L L = 0,5 %

u θ = δ θ θ = 0,667 %

A altura é dada por:

H = L tan ⁡ θ = 17,32 m

Já a incerteza, é dada por:

u H = L H ∂ H ∂ L   u L 2 + θ H ∂ H ∂ θ   u θ 2

Também sabemos que:

∂ H ∂ L = tan ⁡ θ = L 1 + tan ⁡ θ 2

Substituindo na equação:

u H = L H tan ⁡ θ   u L 2 + L θ H 1 + tan ⁡ θ 2   u θ 2

u H = 0,949 %

δ H = u H H = 0,164 m

Passo 2

Para avaliarmos o ângulo, vamos utilizar a tabela auxiliar a seguir:

Usando o Excel, teremos:

θ = 31,4 → u H = 0,947 %

Para traçarmos o gráfico pedido, vamos usar a expressão:

u H θ = tan ⁡ θ δ L H 2 + δ θ tan ⁡ θ 1 + tan ⁡ θ 2   2

Utilizando algum programa para fazer o gráfico:

Resposta

H = 17,32 m

u H = 0,949 %

θ = 31,4 → u H = 0,947 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a velocidade do som no vapor a 200° C e 400k P a (a) pela aproximação de gás ideal ( T a b e l aA . 4 ) e (b) usando o software E E S (ou as tabelas de vapor) e fazendo pequenas alterações ise
O volume v de um cilindro circular reto deve ser calculado por meio do raio da base R e altura H . Se a incerteza em R é 2 % e a incerteza em H é 3 % , calcule a incerteza total no volume calculado.
Mesmo uma pequena quantidade de gás dissolvido pode mudar drasticamente a velocidade do som de uma mistura gás-líquido. Estimando a mudança pressão-volume da mistura, Olson [ 51 ] fornece a seguinte f
O dispositivo da Figura P1.54 é chamado de viscosímetro de disco rotativo [29]. Considere que R = 5 cm e h = 1 mm. (a) Se o torque requerido para girar o disco a 900 rpm for 0,537 N.m, qual é a viscos
Use a teoria do Problema 1.49 para um eixo de 8 cm de comprimento, girando a 1.200 rpm, com r i =2,00c mer o =2,05c m . (a) Se o torque medido for 0,293 N.m, qual é a viscosidade do fluido? (b) Consid