Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 79
Mesmo uma pequena quantidade de gás dissolvido pode mudar drasticamente a velocidade do som de uma mistura gás-líquido. Estimando a mudança pressão-volume da mistura, Olson [] fornece a seguinte fórmula aproximada:
na qual é a fração em volume do gás, é o módulo de elasticidade volumétrica e os subscritos e representam líquido e gás, respectivamente. (a) Mostre que a fórmula é dimensionalmente homogênea. (b) Para o caso especial de bolhas de ar (densidade de e pressão de ) na água (densidade de e módulo de elasticidade volumétrica , faça o gráfico da velocidade do som na mistura no intervalo e discuta.
Passo 1
E aí, tudo bem? Bora matar essa questão comigo!
a)
Primeiro verificando a homogeneidade, sendo a velocidade do som em temos:
Sim, nossa formula é homogênea!
Passo 2
b)
Agora vamos montar um gráfico para a variação de
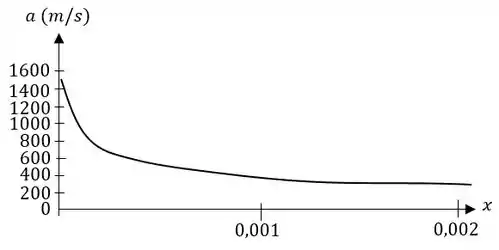
A diferença na compressibilidade entre a água e o ar é tão grande que a queda da velocidade é muito acentuada!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
a)
Sim, nossa formula é homogênea!
b)
Gráfico vide passo a passo
A diferença na compressibilidade entre a água e o ar é tão grande que a queda da velocidade é muito acentuada!