Repita o Exemplo , no caso em que a parede está se movendo para cima com velocidade . Como verificação, certifique-se de que o seu resultado coincida com aquele do Exemplo quando . Torne a sua equação do perfil de velocidades adimensional utilizando a mesma normalização do Exemplo , e mostre que aparece um número de Froude e um número de Reynolds. Faça o gráfico do perfil versus para casos em que e , e . Discuta.
Passo 1
Vamos começar desenhando a figura do Exemplo , tomando o cuidado de agora considerar que a parede se move a uma velocidade :
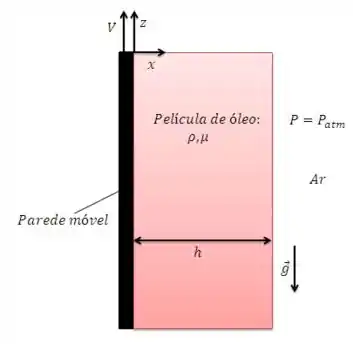
Assim como no Exemplo devemos obter o perfil de velocidades para esta situação. Vamos lá?
O primeiro passo para isso será aplicar a equação da continuidade em coordenadas cartesianas:
Para resolver, vamos considerar que temos um escoamento estacionário e um fluido incompressível de propriedades constantes. Além disso, a única componente de velocidade não nula é . Então:
E a equação da continuidade se reduz à:
Ou seja, a velocidade não é função da direção . O que é equivalente a dizer:
Nosso próximo passo para obter o perfil de velocidades será aplicar a equação de Navier-Stokes.
Passo 2
Como o óleo está escoando na direção , vamos usar agora a equação de Navier-Stokes para esta componente:
Para resolver vamos agora olhar mais de perto para cada termo.
Começando pelo lado esquerdo. Estamos considerando um processo estacionário e as componentes de velocidade e são nulas. Além disso, vimos pela equação da continuidade que . Então:
Assim, o lado esquerdo da equação se reduz à:
Tudo bem até aqui?
Vamos agora olhar para os termos do lado direito. Vamos assumir que o fluido escoa devido à força da gravidade e, pela movimentação da parede. Ou seja, o gradiente de pressão é desprezível.
Pela figura, podemos ver que a gravidade atua na direção . Além disso, pela equação da continuidade concluímos que . Então:
E a nossa equação fica:
Passo 3
Para continuar, vamos agora integrar a equação em relação à :
Para obter podemos aplicar uma condição de contorno. Na interface óleo-ar a tensão superficial é mínima. Certo?
Então, se o atrito é mínimo, esperamos que a velocidade máxima aconteça em .
Ou seja:
Substituindo na relação anterior:
Para continuar, vamos integrar novamente em relação à :
Novamente, para obter a constante vamos aplicar a segunda condição de contorno. Tudo bem?
Pela hipótese da aderência a velocidade do fluido em contato com a parede deve ser igual à velocidade da parede. Ou seja:
Substituindo no perfil:
Passo 4
Vamos começar verificando se nosso perfil coincide com o obtido no Exemplo . Fazendo , nosso perfil se reduz à:
Rearranjando:
Que é o mesmo resultado do Exemplo .
Agora que confirmamos o nosso resultado, vamos fazer a adimensionalização da equação:
Voltando para o perfil:
Agora que aplicamos a adimensionalização, precisamos ainda mostrar que aparecerão um número de Reynolds e um número de Fraude. Este será o nosso próximo passo.
Passo 5
O número de Fraude é dado por:
E o número de Reynolds é:
Vamos retornar ao perfil e tentar chegar nessas relações. Tudo bem?
Para finalizar, vamos fazer os perfis versus para os casos em que e , e .
Passo 6
Com o auxílio de Excel podemos plotar os gráficos das funções:
E
Devemos obter algo da forma:
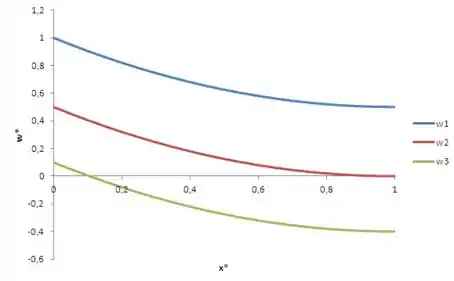
A partir dos gráficos podemos ver a taxa com que a velocidade adimensional decresce independe da relação , já que a relação corresponde ao coeficiente linear da curva .
Resposta
Perfil de velocidade:
Perfil de velocidade adimensionalizado: