Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 81

Analise a influência de uma espessura de placa não nula no Exemplo 11.2, quando há 40 canais.

( a ) Determine as dimensões externas, L , do núcleo do trocador de calor para uma espessura de placa igual a t   =   0,8   m m , considerando placas de alumínio puro ( k A l   =   237   W / ( m   ·   K ) ) e de fluoreto de polivinilideno ( P V D F ,   k p v   =   0,17   W / ( m   ·   K ) ) . Despreze as espessuras das placas exteriores superior e inferior.

b Represente graficamente a dimensão do núcleo do trocador como uma função da espessura das placas para o alumínio e para o PVDF no intervalo 0   ≤   t   ≤   1   m m .

Passo 1

Temos aqui um problema, onde temos que analisar a influência de uma espessura de placa não nula no Exemplo 11.2.

Retirando alguns dados do Exemplo e da questão ( a ) , temos a seguinte representação:

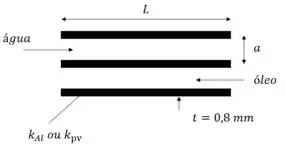
Onde temos N = 40   c a n a i s . Do exemplo 1.2, temos os seguintes dados:

T h , e n t = 100 ℃ ,   T h , s a i = 60 ℃ ,   T c ,   s a i = 30 ℃ ,   m ˙ h = 0,1 k g s ,   m ˙ c = 0,2 k g s

Passo 2

Note que não temos a temperatura de filme da água, e também não podemos determina-la, pois não temos T c , e n t , mas do exemplo 11.2, temos uma estimação para a temperatura de filme:

T c - ≈ 35 ℃

Da tabela A-6 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.):

μ = 725 × 10 - 6 N ∙ s m 2 ,   k = 0,625 W m ∙ K .

Para o óleo, temos que a temperatura de filme é:

T - h = T h ,   e n t + T h ,   s a i 2 = 100 + 60 2 = 80 + 273 = 353   K

Da tabela A-5 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.):

μ = 3,25 × 10 - 2 N ∙ s m 2 ,   k = 0,138 W m ∙ K

E por fim, do enunciando, temos que:

k A l = 237 W m ∙ K ,   k p v = 0,17 W m ∙ K

Passo 3

Então bora lá galera, começando então pela questão ( a ) , precisamos determinar as dimensões externas, L , do núcleo do trocador de calor para uma espessura de placa igual a t   =   0,8   m m .

Além disso, no processo de determinar esses parâmetros, podemos desprezar as espessuras das placas exteriores superior e inferior.

Para começarmos a resolução, nós temos uma ajudinha do exemplo 11.2, onde iremos assumir que o fluido ainda é laminar, além disso o exemplo nos traz:

N u D = h D h k = 7,54

Portanto, determinando os coeficientes de transferência de calor...

h c   = 7.54 k D h   = 7.54 k 2 a

h c a   =   7.54   ×   0.625 W m ⋅ K 2     =   2.36 W m ⋅ K

h h   = 7.54 k D h   = 7.54 k 2 a

h h a   =   7.54   ×   0.138 W m ⋅ K   2   =   0.520 W m ⋅ K

Passo 4

Assim como a maioria dos problemas de transferência de calor, principalmente os que envolve projetos, precisamos determinar o coeficiente global de transferência de calor.

Desprezar as espessuras das placas exteriores superior e inferior. Temos...

1 U A = 1 h c A + t k A L A + 1 h h A

1 U = 1 h c + t k A L + 1 h h

1 U = a h c a + t k A L + a h h a

onde h c a e h h a são constantes dadas pelo Passo 3.

Passo 5

Assim como no exemplo 11.2, iremos precisar dos dados do exemplo 11.1, sendo eles a diferença de temperatura média logarítmica necessária e a taxa de transferência de calor:

∆ T l m = 43,2   ℃

q = 8524   W

Usando também...

A = N - 1 L 2

Portanto, nosso coeficiente global de transferência de calor se torna:

1 U = A ∆ T l m q = 39 × 43,2 ℃ × L 2 8524   W = 0,198 K W L 2

Passo 6

Note que a dimensão do núcleo, L , está relacionada à dimensão da folga, a e espessura da placa, t (não levando em conta as placas externas), temos que:

L = N a + ( N - 1 ) t

Logo, teremos...

1 U = 0,198 K W N a + N - 1 t 2

Agora voltando na nossa equação, inicial para o coeficiente global...

1 U = a h c a + t k A L + a h h a

A equação se torna...

a h c a + t k A L + a h h a = 0,198 K W N a + N - 1 t 2

Ampliando o lado direito da igualdade...

0,198 K W N 2 a 2 + 2 0,198 K W N N - 1 t a + 0,198 K W N - 1 2 t 2

Passo 7

Você está indo muito bem, agora note que podemos resolver a equação quadrática resultante para a, pois podemos separar os termos e aplicar a equação de bhaskara...vem comigo.

A equação é um pouco grande, mas podemos juntar o lado esquerdo com o lado direto e ter uma equação do tipo:

A a 2 + B a + C = 0

Que pode ser resolvida por:

a = - B ± B 2 - 4 A C 2 A

Separando os termos da equação...

A = 0,198 K W N 2 = 0,198 K W × 40 2 = 316   K W

B = 2 0,198 K W N N - 1 t - 1 h c a - 1 h h a

B = 0,395 K W × 40 × 39 × 0,0008   m - 1 2,36 W m ∙ K - 1 0,520 W m ∙ K

C = 0,198 W K N - 1 2 t 2 - t k A L

C = 0,198 K W 39 2 0,0008   m 2 - 0,0008   m 237 W m ∙ K = 1,89 × 10 - 4 m 2 ∙ K W

Passo 8

Isso ai!!

Agora que temos nossos valores separados e determinado, podemos resolver a equação a baixo:

a = - B ± B 2 - 4 A C 2 A

a = 1,85 ± 1,85 2 - 4 × 316 × 1,89 × 10 - 4 2 × 316 = ,

a = 1,04 × 10 - 4   m

o u

a = 0 ,   0058   m

Passo 9

Agora, voltando para nossa equação para L ...

L = N a + ( N - 1 ) t

Substituindo os valores encontrados...

L = 40 1,04 × 10 - 4   m + 40 - 1 0,0008   m

L = 0,0354   m

o u

L = 40 0 ,   00 58   m + 40 - 1 0,0008   m

L = 0 , 263   m

Passo 10

Para o outro material, basta repetimos os cálculos anteriores, ou seja...

a h c a + t k p v + a h h a = 0,198 K W N a + N - 1 t 2

Ampliando o lado direito da igualdade...

0,198 K W N 2 a 2 + 2 0,198 K W N N - 1 t a + 0,198 K W N - 1 2 t 2

Passo 11

A equação é um pouco grande, mas podemos juntar o lado esquerdo com o lado direto e ter uma equação do tipo:

A a 2 + B a + C = 0

Que pode ser resolvida por:

a = - B ± B 2 - 4 A C 2 A

Separando os termos da equação...

A = 0,198 K W N 2 = 0,198 K W × 40 2 = 316   K W

B = 2 0,198 K W N N - 1 t - 1 h c a - 1 h h a

B = 0,395 K W × 40 × 39 × 0,0008   m - 1 2,36 W m ∙ K - 1 0,520 W m ∙ K

C = 0,198 W K N - 1 2 t 2 - t k p v

C = 0,198 K W 39 2 0,0008   m 2 - 0,0008   m 0,17   W m ∙ K = - 4,51 × 10 - 3 m 2 ∙ K W

Passo 12

Isso ai!!

Agora que temos nossos valores separados e determinado, podemos resolver a equação a baixo:

a = - B ± B 2 - 4 A C 2 A

a = 1,85 ± 1,85 2 - 4 × 316 × ( - 4,51 × 10 - 3 ) 2 × 316 = ,

a = 7,71 × 10 - 3   m

o u

a = - 1,85 × 10 - 3   m

Passo 13

Agora, voltando para nossa equação para L ...

L = N a + ( N - 1 ) t

Substituindo o único valor positivo encontrado...

L = 40 7,71 × 10 - 3   m + 40 - 1 0,0008   m

L = 0 , 340   m

Resposta

( a ) O valor de L para k A L é:

L = 0,0354   m

o u

L = 0,263   m

O valor de L para k p v é:

L = 0,340   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trocador de calor de casco e tubo é utilizado para resfriamento 47 k g s de fluido em um processo de vapor escoando através dos tubos de 160°C a 100°C. O trocador de calor tem o total de 100 tubos
Durante um experimento, um trocador de calor de placas utilizado para transferir calor da água quente para a água fria é testado, e as medições são as seguintes:A área de transferência de calor é calc
Um trocador de calor de casco e tubo com 2 passes no casco e 4 passes no tubo é usado para resfriar o óleo c p = 2,0 k J k g K de 125°C a 55°C. O fluido de resfriamento é a água, que entra no lado do
Um trocador de calor com 2 passes no casco e 4 passes no tubo é usado para aquecimento de hidrocarboneto c p = 2,0 k J k g K permanentemente de 20°C para 50°C. Água entra no lado do casco a 80°C e o d
Em um trocador de calor líquido-líquido de escoamento paralelo, as temperaturas de entrada e saída do fluido quente são 150 ℃ ℃ e 90 ℃ ℃, enquanto as do fluido frio são 30 ℃ ℃ e 70 ℃ ℃, respectivament