Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 27
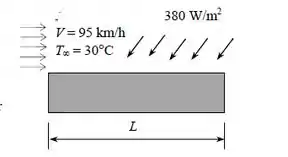
A superfície superior de um vagão de passageiros de um trem em movimento na velocidade de 95 km/h tem 2,8m de largura e 8 m de comprimento. A superfície absorve radiação solar a uma taxa de 380 W/m², e a temperatura do ar ambiente é de 30°C. Pressupondo que o teto do vagão seja perfeitamente isolado e que a troca de calor por radiação com as imediações seja pequena em relação à convecção, determine a temperatura de equilíbrio da superfície superior do vagão.
Passo 1
O enunciado nos diz que podemos desprezar o calor trocado por convecção e é isto que faremos. Além disso, ele já nos deu o valor de q’’, você se ligou?
Quando ele diz o quanto que a superfície absorve de energia, ele está dizendo que q’’ = 380W/m² !
O que o problema quer então é que a gente calcule Ts a partir da equação de taxa de calor por convecção, sacou?
IMPORTANTE: Outra parada que você tem que ficar esperto são as unidades de q, q’ e q’’.
O que ele nos deu foi q’’ que nada mais é do que q/A, belê?
Passo 2
Vamos calcular h usando a correlação apropriada, mas antes, bora calcular Reynold com as propriedades do ar em .
EITA CARACA, COMO VOU CALCULAR Tf SE EU PRECISO DE TS ???
Calma, esse é um típico problema de transcal.
O que você vai fazer é chutar uma Ts usando O BOM SENSO PELAMOR DE GOD. Eu vou chutar Ts = 30°C porque o problema diz que quer o valor em equilíbrio térmico e no equilíbrio Ts = Too, beleza?
Estamos acima do valor crítico e portanto num regime combinado (laminar + turbulento)
Passo 3
Tomamos a correlação adequada:
Passo 4
Agora é só substituir na nossa equação de Ts
ENTENDENDO A RESPOSTA: Você percebeu que meu Ts não deu um valor igual ao que eu chutei, né?
O que eu teria que fazer então? Agora, com esse novo Ts eu calcularia uma nova Tf, tomaria de novo as propriedades na temperatura de filme nova, calcularia Reynold, o coeficiente de transferência de calor por convecção e recalcularia por fim uma nova Ts.
Teríamos que fazer esse procedimento até que a Ts usada para calcular Tf seja igual a temperatura que você encontrará ao final do procedimento.
Mas fica tranquilo que seu professor no máximo vai pedir pra você escrever o que você faria (igual eu falei agora) ao invés de ficar fazendo cálculo iterativo até não aguentar mais haha