Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 51

Uma aproximação para a forma da camada-limite nas Figuras 1.6 b e P 1.51 é a fórmula

u y ≈ U sen ⁡ π y 2 δ ,   0 ≤ y ≤ δ

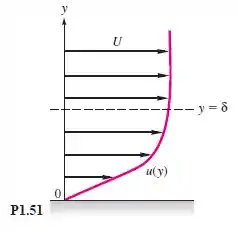
em que U é a velocidade da corrente longe da parede e d é a espessura da camada-limite, como na Figura P 1.51 . Se o fluido for o hélio a 20   ° C e 1   a t m , e se U = 10,8   m / s e d = 3   c m , use a fórmula para (a) calcular a tensão de cisalhamento τ p na parede em P a e (b) encontre a posição na camada-limite em que τ é metade de τ p .

Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

a)

Para começar vamos coletar os dados do hélio na nossa conhecida tabela A . 4 , para as T = 20 ° C , R = 2077   m 2 s 2 ⋅ K e μ = 1,97 ⋅ 10 - 5   k g m ⋅ s

Temos que:

τ = μ d u d y

Mas a equação da velocidade é:

u y ≈ U sen ⁡ π y 2 δ

Vamos derivar!

τ p = μ U π 2 δ ⋅ cos ⁡ π y 2 δ y = 0 = μ U π 2 δ

Substituindo pelos valores dados:

τ p = 1,97 ⋅ 10 - 5   k g m ⋅ s ⋅ 10,8   m s ⋅ π 2 ( 0,03   m )

τ p = 1 , 1   P a

Passo 2

b)

Como já descobrimos antes, a variação da tensão de cisalhamento através da camada limite é em função do cosseno, vamos organizar um pouco essa equação!

τ y = μ U π 2 δ ⋅ cos ⁡ π y 2 δ

τ y = τ p cos ⁡ π y 2 δ

Como a questão nos pede o valor de y para τ y = τ p 2 , teremos o seguinte:

τ p cos ⁡ π y 2 δ = τ p 2

cos ⁡ π y 2 δ = 1 2

Logo:

π y 2 δ = π 3

Isolando y :

y = 2 δ 3

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

  1. τ p = 1 , 1   P a
  2. y = 2 δ 3
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a mangueira de jardim da Figura 2.5. Suponha que o campo de velocidade é dado por V → = u 0 î +v 0 s e n [ ω ( t-x / u 0) ] j ^ î , onde a direção x é horizontal e a origem está na posição m
As linhas de emissão são visualizadas por meio de um fluido corante de empuxo neutro injetado em um campo de escoamento a partir de um ponto fixo no espaço. Uma partícula do fluido corante que está no
Um escoamento é descrito pelo campo de velocidade V =a x i+b j , em que a=1 / 5s- 1 b=1m / s . As coordenadas são medidas em metros. Obtenha uma equação para a linha de corrente que passa através do p
Um escoamento é descrito pelo campo de velocidade V =a y i+b t j , em que a=0,2s - 1 e b=0,4 m / s 2 . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (1, 2) em t = 0. Em t=3s ,
Um escoamento é descrito pelo campo de velocidade V =a i+b x j , em que a=2m / s e b=1s- 1 . As coordenadas são medidas em metros. Obtenha a equação para a linha de corrente que passa pelo ponto ( 2 ,