Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 26

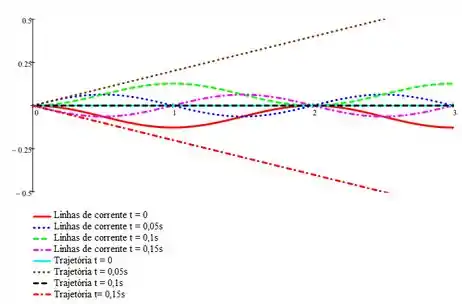
Considere a mangueira de jardim da Figura 2.5. Suponha que o campo de velocidade é dado por V → = u 0 î +   v 0     s e n [ ω ( t   -   x / u 0   ) ] j ^   , onde a direção x é horizontal e a origem está na posição média da mangueira, u 0 = 10   m / s , ν 0   = 2   m / s , e ω   =   5   ciclos / s . Determine e trace em um gráfico as linhas de corrente instantâneas que passam através da origem em t = 0   s , 0,05   s , 0,1   s e 0,15   s . Também determine a trace um gráfico com as trajetórias das partículas que deixam a origem para os mesmos quatro instantes de tempos.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede as linhas de corrente instantâneas que passam através da origem em t = 0   s , 0,05   s , 0,1   s e 0,15   s . E também, determine a trace um gráfico com as trajetórias das partículas que deixam a origem para os mesmos quatro instantes de tempos . Primeiro, para as equações das linhas de corrente:

v u = d y d x = v 0 sin ⁡ ω t - x u 0 u 0 d y = v 0 sin ⁡ ω t - x u 0 u 0 d x

Integrando: y = v 0 cos ⁡ ω t - x u 0 ω + c

Agora, sabemos que para y = 0 , temos x = 0 . Logo, substituindo, temos:

y = v 0 cos ⁡ ω t - x u 0 - cos ⁡ ( ω t ) ω

Passo 2

Agora, para determinarmos a trajetória, vamos encontrar x ( t ) :

d x d t = u 0

Separando as variáveis e integrando:

d x = u 0   d t x = u 0 t + c 1

Para a condição inicial x = 0 e t = τ :

c 1 = - u 0 τ

Logo:

x = x 0 ( t - τ )

Para y t , temos: d y d t = v = v 0 sin ⁡ ω t - x u 0 d y d t = v 0 sin ⁡ ( ω τ )

Novamente, separando as variáveis e integrando:

d y = v 0 sin ⁡ ω τ d t y = v 0 sin ⁡ ( ω τ ) t + c 2 y = 0 e t = τ :

c 2 = - v 0 sin ⁡ ω τ τ y = v 0 sin ⁡ ω τ ( t - τ )

Passo 3

Por fim, para a trajetória, temos:

x t , τ = u 0 t - τ y t , τ = v 0 sin ⁡ ω τ ( t - τ )

Portanto, nossos gráficos ficam assim:

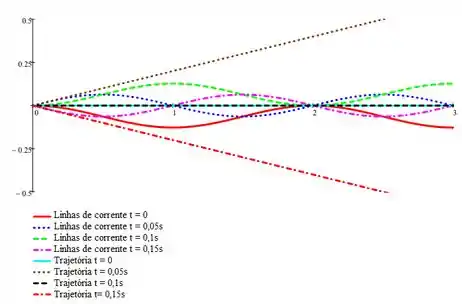
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um modelo simples e popular para os dois fluidos não newtonianos da Figura 1.9a é a lei de potência: τ ≈ C d u d y n em que C e n são constantes ajustadas ao fluido [ 16 ] . Da Figura 1.9 a , deduza o
Um bloco de peso P está sendo puxado sobre uma mesa por um outro peso P 0 , como mostra a Figura P 1.55 . Encontre uma fórmula algébrica para a velocidade constante U do bloco se ele desliza sobre um
Uma aproximação para a forma da camada-limite nas Figuras 1.6 b e P 1.51 é a fórmula u y ≈ U sen ⁡ π y 2 δ ,0 ≤ y ≤ δ em que U é a velocidade da corrente longe da parede e d é a espessura da camada-li
Dada a distribuição de velocidade permanente, incompressível, V = 3 x i + C y j + 0 k , em que C é uma constante, a tensão de cisalhamento τ x y no ponto (x, y, z) é dada por: 3 μ 3 x + C y μ 0 C μ 3
Para a geometria do Problema P1.55, (a) resolva o problema transitório U(t), em que o movimento do bloco começa a partir do repouso e acelera até a velocidade constante final U 0 do Problema P1.55. (b