Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 29
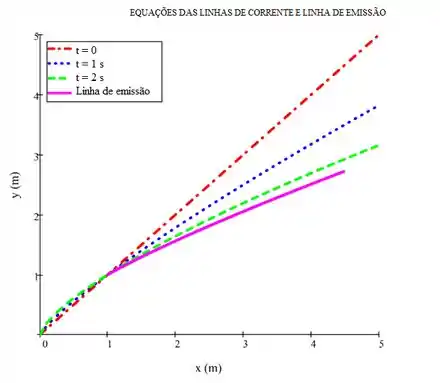
As linhas de emissão são visualizadas por meio de um fluido corante de empuxo neutro injetado em um campo de escoamento a partir de um ponto fixo no espaço. Uma partícula do fluido corante que está no ponto no instante t deve ter passado pelo ponto de injeção em algum instante anterior . O histórico de uma partícula corante pode ser determinado pela solução das equações da trajetória para as condições iniciais , , quando . As localizações atuais das partículas sobre a linha de emissão são obtidas fazendose τ igual a valores na faixa . Considere o campo de escoamento , em que e . As coordenadas são medidas em metros. Trace a linha de emissão que passa pelo ponto inicial , durante o intervalo de a . Compare com as linhas de correntes que passam pelo mesmo ponto nos instantes , e .
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiro, temos que encontrar as as equações para trajetória na forma:
Onde , é a posição da partícula no instante . Com isso, temos:
Passo 2
Agora, para determinarmos a trajetória, vamos encontrar :
Separando as variáveis e integrando:
Logo, as trajetórias são dadas por:
Passo 3
Agora, para a linha de emissão, temos:
Onde . Logo:
Passo 4
Por fim, temos que a equação das linhas de corrente são dadas por:
Integrando:
Para a particula no ponto no instante , temos:
Já para :
E para :
Com isso, nosso gráfico fica assim:
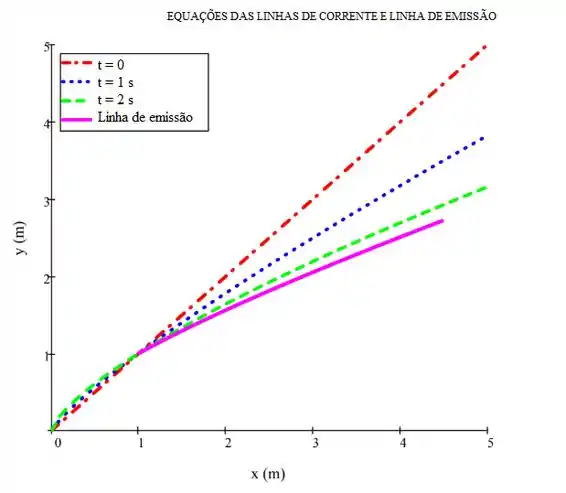
Resposta
