Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 105

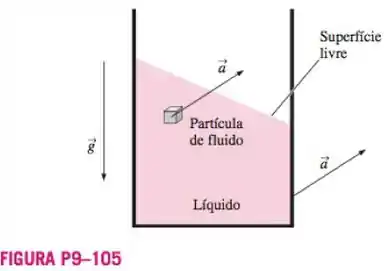
Simplifique a equação de Navier-Stokes o máximo possível para o caso de um líquido incompressível que está sendo acelerado como um corpo rígido em uma direção arbitrária (Fig. P9-120). A gravidade age na direção  - z . Comece com a forma vetorial incompressível da equação de Navier-Stokes, explique como e por que alguns termos podem ser simplificados, e forneça o seu resultado final na forma de uma equação vetorial.

Passo 1

Fala galera!!

Nessa questão, queremos simplificar a equação de Navier-Stokes para o caso da figura descrita no problema. Vamos começar a resolver a partira da equação 9-60 que é a forma vetorial incompressível da equação de Navier-Stokes. Assim temos que:

ρ D V → D t = - ∇ → P + ρ g → + μ ∇ 2 V →                                       E q .   1

Em que  g → é o vetor de gravidade, P  é a pressão, ρ  é a densidade, V →  é o vetor de velocidade.

Passo 2

Nesse problema, temos que a aceleração do material será a aceleração do corpo em movimento. Assim, podemos dizer que

D V → D t = a →                                 E q .   2

Temos também que o líquido está sendo acelerado como um corpo rígido. Portanto, não há movimento relativo entre as partículas de fluido, logo o termo viscoso pode ser negligenciado. Ou seja:

μ = 0                                   E q . 3

Pela figura mostrada no enunciado, podemos perceber que a gravidade está atuando na direção negativa de z . Assim, podemos dizer que:

g → = - g k →                               E q . 4

Passo 3

Pelas considerações feitas no passo anterior, podemos substituir as equações (2), (3) e (4) na equação (1). Assim temos:

ρ D V → D t = - ∇ → P + ρ g → + μ ∇ 2 V →

ρ a → = - ∇ → P + ρ - g k →   + 0 ∇ 2 V →

ρ a → = - ∇ → P - ρ g k →

- ρ a → = ∇ → P + ρ g k →

Portanto, temos que a equação de aceleração do corpo rígido é dada por:

- ρ a → = ∇ → P + ρ g k →

Resposta

- ρ a → = ∇ → P + ρ g k →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é significativo nas curvas com função corrente constante? Explique por que a função corrente é útil na mecânica dos fluidos.
Considere o escoamento bidimensional no plano x y .Qual é o significado da diferença do valor da função corrente Ψ de uma linha de corrente para outra?
Considere o campo de velocidade pemanente, bidimensionaldado por V → =u ,v =1,3+2,8 x i →+1,5—2,8 y j → . Verifique se esse campo de escoamento é incompressível.
Imagine escoamento incompressível, permanente, bidimensional que é puramente circular no plano x y ou r θ . Em outras palavras, a componente de velocidade u θ é diferente de zero, mas u r é zero era t
Que restrições ou condições são impostas na função corrente Ψ de maneira que ela satisfaça exatamente a equação da continuidade bidimensional incompressível por definição? Porque essas restrições são