Um aquecedor de ar é constituído por um tubo de aço com raios interno e externo e , respectivamente, e oito aletas longitudinais usinadas no tubo, cada uma com espessura . As aletas se estendem até um tubo concêntrico, que possui raio e está isolado na sua superfície externa. Água, a uma temperatura , escoa através do tubo interno, enquanto ar, a , escoa através da região anular formada pelo tubo com maior diâmetro.

(a) Esboce o circuito térmico equivalente do aquecedor e relacione cada resistência térmica aos parâmetros apropriados do sistema.
(b) Sendo e qual é a taxa de transferência de calor por unidade de comprimento?
(c) Avalie o efeito na taxa de transferência de calor causado pelo aumento no número de aletas e/ou na espessura das aletas , sujeitos à restrição
Passo 1
Bora pra mais uma questão? \o/. Aqui nós temos as condições geométricas e de convecção do aquecedor de ar de tubo concêntrico com aletas internas. E queremos calcular encontrar o circuito térmico, a taxa de calor por unidade de comprimento do tubo e o efeito de alterações na matriz de aletas.
Passo 2
Para resolver essa questão, vamos assumir que: estamos em condição de estado estacionário, a transferência de calor é unidimensional na direção radial, k é constante e a superfície externa é adiabática.
Na letra (a), nós queremos o circuito térmico que é mostrado esquematicamente abaixo.

Onde,
E,
Passo 3
Na letra (b) queremos a taxa de transferência de calor por unidade de comprimento. Para isso, vamos analisar primeiro a troca de calor:
Substituindo as condições conhecidas, temos que:
Onde então:
Passo 4
Na letra (c), queremos o efeito na taxa de transferência de calor causado por alterações na matriz de aletas. O pequeno valor de sugere que se pode obter algum benefício aumentando , bem como aumentando .
Com a exigência de , ao aumentar de para , aumenta de para . Portanto, para fixo, aumenta com o aumento de . No entanto, do ponto de vista da maximização do , é preferível usar o maior número de aletas mais finas. Portanto, sujeito à restrição prescrita, escolheríamos e , para os quais.
Resposta
(a)
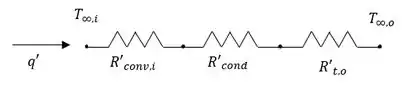
(b)
(c) Para fixo, aumenta com o aumento de . Sujeito à restrição prescrita, escolheríamos e , para os quais.