Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 157
Aletas de alumínio com perfil triangular estão fixadas a uma parede plana cuja temperatura na superfície é de . A espessura da base das aletas é de e o seu comprimento é de . O sistema encontra-se em um ambiente a uma temperatura de , com um coeficiente de transferência de calor na superfície de
(a) Quais são a eficiência e a efetividade das aletas?
(b) Qual é o calor dissipado por unidade de largura em uma única aleta?
Passo 1
Vamos fazer mais uma questão de aletas 😊. Aqui, nós temos as dimensões, temperatura básica e condições ambientais associadas a uma aleta triangular de alumínio (ou como meu professor costumava chamar, “estaca de vampiro”). Ilustrando esse problema, temos:
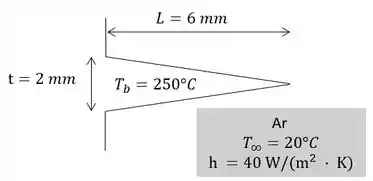
Onde queremos encontrar a eficiência e efetividade da aleta. Além da dissipação de calor por unidade de largura.
Passo 2
Para resolver essa questão, vamos assumir que:
(1) Estamos em condição de estado estacionário;
(2) A condução é unidimensional;
(3) As propriedades são constantes;
(4) A resistência à radiação e ao contato de base é desprezível;
(5) O coeficiente de convecção é uniforme.
Na letra (a) queremos saber a eficiência e a efetividade da aleta. Com:
Encontramos:´
Onde o valor de foi retirado da Tabela A.1 para o alumínio puro à
Passo 3
Pela Fig. 3.19 temos que Consequentemente,
E a efetividade da aleta é:
Substituindo os valores:
Passo 4
Na letra (b) queremos o calor dissipado por unidade de largura em uma única aleta, que pode ser escrito como:
Resposta
- e