Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 93
Um aquecedor elétrico cuja resistência é um fio extenso e homogêneo de raio é usado para aquecer o ar de uma sala pela passagem de corrente elétrica no fio. Calor é gerado no fio uniformemente a uma taxa de como resultado da resistência que a corrente encontra. Considerando que a temperatura da superfície externa do fio permanece a 180 °C, determine a temperatura a depois de alcançadas as condições de operação permanente. Assuma que a condutividade térmica do fio é .
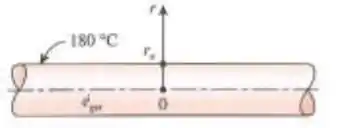
Passo 1
O nosso primeiro passo é fazer considerações para resolver o nosso problema. Sendo assim, temos um problema de regime permanente, com condução de calor unidimensional, geração de calor e condutividade térmica constante.
Inicialmente, vamos resolver a EDO associada, obtendo assim a distribuição de temperatura. Somente depois iremos obter a temperatura para um valor de . Como estamos trabalhando com um fio de formato cilíndrico, vamos utilizar o sistema de coordenadas cilíndrica. Portanto, a EDO que rege o nosso problema é:
Agora, precisamos discutir as condições de contorno que o nosso problema está sujeito, os quais são dois. O primeiro é a simetria do fio. Esta simetria implica em dizer que a temperatura máxima do fio está localizada no meio dele. Consequentemente, não há condução de calor em . Portanto:
Já a outra condição é temperatura constante na superfície. Portanto, temos:
Passo 2
Agora, precisamos resolver a nossa EDO e utilizar as condições de contorno, pois, determinar a variação de temperatura na placa nada mais é do que determinar a distribuição de temperatura nela. Portanto, temos:
Vamos utilizar a nossa primeira condição de contorno, a simetria do problema. Com isto, temos:
Logo,
Agora que descobrimos o valor da primeira constante, vamos continuar a resolver a nossa EDO. Portanto:
Precisamos utilizar a nossa segunda condição de contorno. Portanto, temos:
Portanto, a distribuição de temperatura no nosso fio é:
OBS: Muito cuidado na hora de substituírem as constantes do problema! Sempre tomem cuidado com as unidades que estamos trabalhando. Tentem sempre colocar no SI.
Passo 3
Estamos quase terminando a nossa questão! Agora que obtivemos a distribuição de temperatura, basta substituirmos o valor na equação para obtermos a temperatura. Entretanto, muito cuidado! A unidade tem que estar no SI, então, substituiremos . Agora sim. Portanto, temos:
Percebam que a resposta variou um pouco em relação ao resultado do livro apenas pelos arredondamentos dos números.