Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 82
Reconsidere o Prob. 2-81. Usando a relação obtida para a variação da temperatura no cilindro, trace a temperatura como função do raio r no intervalo de a e discuta os resultados. Use EES (ou outro programa).
Passo 1
O nosso primeiro passo é relembrar a distribuição de temperatura na questão anterior. Com isto, temos:
Agora, vamos substituir os valores das constantes dadas na questão anterior. Com isto, temos:
Não se esqueçam de transformar as unidades para o SI!
Passo 2
Agora que obtivemos a função, vamos plotar o gráfico da nossa função. Sendo assim, temos:
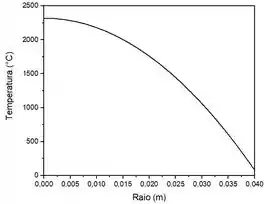
Como esperado, à medida que nos afastamos do centro, a temperatura diminui.
Resposta
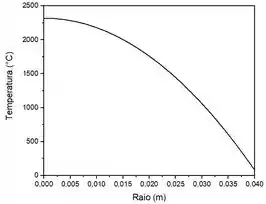
A temperatura diminui à medida que nos afastamos do centro do fio.
Exercícios de Livros Relacionados
Uma maçã de raio R perde calor de forma constante e uniforme da superfície externa para o ar ambiente a uma temperatura T ∞ com coeficiente de convecção h e para as superfícies ao redor a uma temperat
Gera-se calor uniformemente em uma barra sólida de 4 cm de diâmetro e 12 cm de comprimento ( k = 2,4W / m ⋅ K ) . As temperaturas no centro e na superfície da barra são 210 e 45 °C, respectivamente. A
Qual das expressões seguintes é a correta para uma equação de condução de calor unidimensional e permanente para um cilindro com geração de calor e condutividade térmica constante? 1 r ∂ ∂ r r k ∂ T ∂
Considere uma extensa parede plana de espessura L, condutividade térmica k e área da superfície A. A superfície esquerda da parede está exposta ao ar ambiente a temperatura T ∞ com coeficiente de tran
Uma aleta de 1c m de diâmetro e 30c m de comprimento de alumínio ( k = 237W / m ⋅ K ) está fixada em uma superfície a 80 ℃ ℃. A superfície é exposta ao ar ambiente a 22 ℃ ℃ com coeficiente de transfer