Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 2.Problemas - Ex. 53ab

Um aquecedor elétrico delgado, dissipando 4000   W / m 2 , encontra-se imprensado entre duas placas, com espessura de 25 mm, cujas superfícies expostas trocam calor por convecção com um fluido a T ∞ = 20 ° C   e   h = 400   W / ( m 2 ⋅ K ) . As propriedades termofísicas do material das placas são ρ = 2500   k g / m 3   ,   c = 700   J / ( k g ⋅ K )   e   k   =   5   W / ( m ⋅ K ) .

(a) Em coordenadas T — x, esboce a distribuição de temperaturas no regime estacionário para -   L ≤   x ≤ + L . Calcule os valores das temperaturas nas superfícies, x   =   ±   L , e no plano central, x   =   0 . Identifique essa distribuição como Caso 1 e explique suas características marcantes.

(b) Considere condições nas quais haja uma perda de refrigerante e a existência de uma condição aproximadamente adiabática na superfície x =   + L . Nas coordenadas T   —   x usadas na parte (a), esboce a distribuição de temperaturas no regime estacionário correspondente e indique as temperaturas em x   =   0   e   ± L . Identifique essa distribuição como Caso 2 e explique suas características marcantes.

(c) Com o sistema operando como descrito na parte (b), a superfície x   =   - L também passa por uma perda súbita de resfriamento. Essa situação perigosa passa despercebida por 15 minutos, quando então a potência do aquecedor é desativada. Considerando a inexistência de perda de calor pelas superfícies das placas, qual é a distribuição de temperaturas nas placas após um longo período de tempo t → ∞ ? Esta distribuição é uniforme e em estado estacionário. No seu esboço, mostre essa distribuição como Caso 3 e explique suas características marcantes. Sugestão: Aplique a exigência de conservação de energia em um intervalo de tempo como base, Equação 1.11b, usando as condições inicial e final correspondendo aos Casos 2 e 3, respectivamente.

(d) Em coordenadas T   —   t , esboce o histórico da temperatura, nas posições das placas x = 0   e   ± L , ao longo do período transiente entre as distribuições dos Casos 2 e 3. Onde e quando a temperatura no sistema atinge um valor máximo?

Passo 1

Oii pessoal, show de bola??

“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”

Bora empurrar e macetar essa questãozinha comigo agora

  1. Vamos começar escrevendo a equação de fluxo de calor devido à condução ao longo do eixo x positivo.

    2. q c o n d ' ' = q 0 ' ' 2

    Vamos escrever também a equação do fluxo de calor decido à convecção na superfície

    q c o n v ' ' = h ( T L - T ∞ )

    Na superfície do lado direito da placa, igualaremos os fluxos condutivos e convectivos.

    q 0 ' ' 2 = h ( T L - T ∞ )

    Agora podemos substituir alguns dados numéricos

    4000 2 = 400 T L - 20

    T L = 25 ° C

    Passo 2

    Vamos calcular a temperatura no ponto Médio usando a seguinte expressão:

    q 0 ' ' 2 = k T 0 - T L L

    4000 2 = 5 T 0 - 25 0.025

    T 0 - 25 = 10

    T 0 = 35 ° C

    Como não há isolamento, a temperatura x = - L   também é 25°C

    Passo 3

    Agora para finalizar vamos traçar a distribuição de temperatura - L ≤ x ≤ L

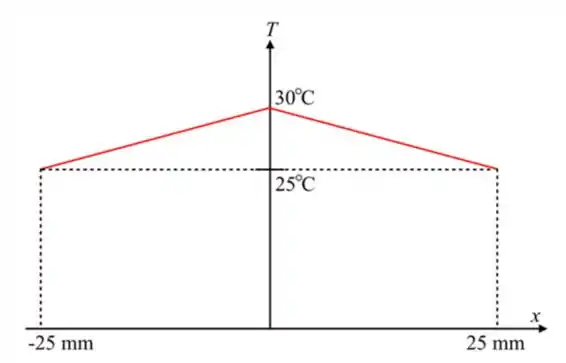
    Passo 4

  2. No caso 2, todo o fluxo de calor gerado será transferido para a extremidade esquerda por cauda da condição adiabática (ou isolamento)

Calculando a temperatura na superfície esquerda da placa

q 0 ' ' = h T - L - T ∞

4000 = 400 ( T - L - 200

T - L - 20 = 10

T - L = 30 ° C

Vamos calcular a temperatura no ponto Médio usando a seguinte expressão:

q 0 ' ' 2 = k T 0 - T - L L

4000 2 = 5 T 0 - 30 0.025

T 0 - 30 = 2 0

T 0 = 50 ° C

Passo 2

Vamos traças a distribuição de temperatura - L ≤ x ≤ L .

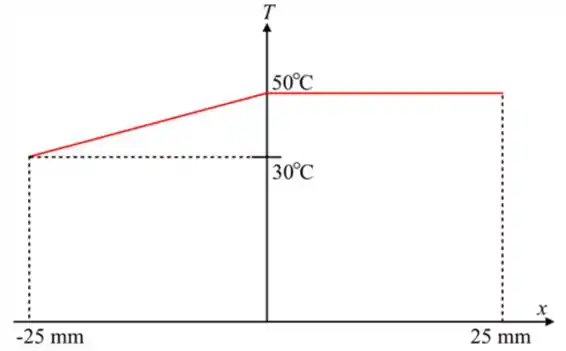
“Faça seus medos terem medo de você”

Resposta

Vide a explicação.

Exercícios de Livros Relacionados

Considere um pequeno, mas conhecido, volume de um metal que tem uma alta condutividade térmica. (a) Como a condutividade térmica é alta, gradientes de temperatura no espaço que se desenvolvem em respo
Considere uma janela com 300m m×300m m em um avião. Para uma diferença de temperaturas de 80 ° C entre as superfícies interna e externa da janela, calcule a perda térmica através de janelas com L=10m
Um método para determinar a condutividade térmica k e o calor específico cp de um material está ilustrado na figura. Inicialmente, as duas amostras idênticas, de diâmetro D=60m m e espessuraL=10m m ,
Condução unidimensional, em regime estacionário e sem geração interna de energia, está ocorrendo em uma parede plana com condutividade térmica constante.A distribuição de temperaturas mostrada no gráf
A superfície interna de uma parede plana é isolada e a superfície externa está exposta a uma corrente de ar a T ∞ . A parede se encontra a uma temperatura uniforme correspondente à da corrente de ar.