Considere um pequeno, mas conhecido, volume de um metal que tem uma alta condutividade térmica. (a) Como a condutividade térmica é alta, gradientes de temperatura no espaço que se desenvolvem em resposta a condições suaves de aquecimento são pequenos. Desprezando gradientes de temperatura, deduza uma equação diferencial que possa ser resolvida para fornecer o comportamento dinâmico da temperatura do metal T ( t ) , se o metal for submetido a uma taxa de transferência de calor constante, q , em sua superfície por um aquecedor elétrico.(b) Um estudante propõe identificar o metal desconhecido através da comparação entre as respostas térmicas medida e predita. Uma vez obtida a coincidência, as propriedades termofísicas relevantes podem ser determinadas e então o metal pode ser identificado pela comparação com dados de propriedades publicados. Esta abordagem funcionará? Considere alumínio, ouro e prata como os metais candidatos

d T d t = q ρ V c p= q V 1 ρ c p Não podemos identificar o material, ou seja, essa abordagem não funcionará.

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 20

Considere um pequeno, mas conhecido, volume de um metal que tem uma alta condutividade térmica.

(a) Como a condutividade térmica é alta, gradientes de temperatura no espaço que se desenvolvem em resposta a condições suaves de aquecimento são pequenos. Desprezando gradientes de temperatura, deduza uma equação diferencial que possa ser resolvida para fornecer o comportamento dinâmico da temperatura do metal se o metal for submetido a uma taxa de transferência de calor constante, , em sua superfície por um aquecedor elétrico.

(b) Um estudante propõe identificar o metal desconhecido através da comparação entre as respostas térmicas medida e predita. Uma vez obtida a coincidência, as propriedades termofísicas relevantes podem ser determinadas e então o metal pode ser identificado pela comparação com dados de propriedades publicados. Esta abordagem funcionará? Considere alumínio, ouro e prata como os metais candidatos

Passo 1

Nessa questão, nós temos o volume de um metal desconhecido de alta condutividade térmica com uma taxa de aquecimento conhecida. Esquematicamente:

E o enunciado está nos pedindo para encontrar a equação diferencial que pode ser usada para determinar a resposta da temperatura do metal ao aquecimento. Além disso, precisamos conferir se o modelo pode ser usado para identificar o metal, com base nas correspondência das respostas térmicas. Então partiu resolver essa questãozinhaaa!

Passo 2

Vamos assumir que os gradientes de temperatura espacial são insignificantes e as propriedades são constantes. Nas quais, as propriedades dos materiais foram pegas na Tabela A.1 , onde:

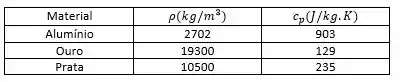
Na letra (a) queremos uma equação diferencial que possa ser resolvida para fornecer o comportamento dinâmico da temperatura do metal . Para isso, vamos fazer um balanço de energia no volume de controle:

Que também pode ser escrito por:

Passo 3

Na letra (b) queremos saber se é possível identificar qual é o tipo de metal. Para isso, vamos calcular o valor de para os três materiais da Tabela A.1.

Como o produto das densidades e dos aquecimentos específicos é muito semelhante para esses três materiais candidatos, em geral, essa abordagem não pode ser usada para distinguir qual material está sendo aquecido.

Resposta

Não podemos identificar o material, ou seja, essa abordagem não funcionará.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um aquecedor elétrico cuja resistência é um fio extenso e homogêneo de raio r 0 = 5m m é usado para aquecer o ar de uma sala pela passagem de corrente elétrica no fio. Calor é gerado no fio uniformeme

Reconsidere o Prob. 2-91. Usando a relação obtida para a variação da temperatura na esfera, trace a temperatura como função do raio r no intervalo de r = 0 a r = r 0 . Trace também a temperatura no ce

Reconsidere o Prob. 2-84. Usando a relação obtida para a variação da temperatura no fio, trace a temperatura no eixo central do fio como função da geração de calor e ˙ g e r no intervalo de 10W / c m

Um longo fio de resistência homogênea, raio r 0 = 0,6c m e condutividade térmica k = 15,2W / m ⋅ K está sendo usado para ferver água em pressão atmosférica pela passagem da corrente elétrica. Calor é

Considere uma esfera homogênea de raio r 0 = 0,04m composta por material radioativo que gera calor a uma taxa constante de e ˙ g e r = 5 × 10 7W / m 3 . O calor gerado é dissipado constantemente para