Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 98

Um aquecedor solar de água é formado por um coletor plano acoplado a um tanque de armazenamento. O coletor tem uma placa de cobertura transparente e uma placa de absorção, que são separadas por uma camada de ar.

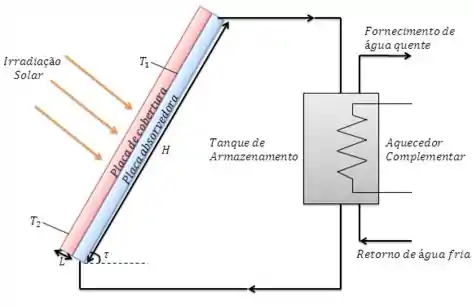
Embora a maior parte da energia solar absorvida na placa de absorção seja transferida para um fluido de serviço que passa através de um tubo em espiral soldado na superfície posterior da placa de absorção, uma parte da energia é perdida por convecção natural e por radiação através da camada de ar. No Capítulo 13 iremos avaliar a contribuição da radiação nesta perda. No momento, restringiremos nossa atenção ao efeito da convecção natural.

(a) Considere um coletor solar inclinado com um ângulo τ = 60 ° e que tem dimensões H = w = 2   m de lado, com uma camada de ar de L = 30   m m . Se as placas de absorção e de cobertura estão a T 1 = 70 ° C e T 2 = 30 ° C , respectivamente, qual é a taxa de transferência de calor por convecção natural saindo da placa de absorção?

Passo 1

Temos a seguinte situação: um coletor solar tem uma placa absorvedora coberta por uma placa de cobertura preenchida com ar. Devemos determinar qual é a taxa de transferência de calor por convecção através da camada de ar dentro da placa de cobertura. Tudo bem?

Então, a taxa de transferência é calculada por:

q = h - A ( T 1 - T 2 )

Precisaremos então obter o coeficiente de convecção natural para esta situação. Para isso, vamos começar calculando a temperatura média do ar dentro da placa de cobertura:

T - m = T 1 + T 2 2

T - m = 70 + 30 2

T - m = 50 ° C = 323   K

As propriedades do ar nesta temperatura são (Tabela A-4, apêndice A):

ρ = 1,0849   k g / m 3

c p = 1007,9   J / k g K

ϑ = 18,20 × 10 - 6   m 2 / s

k = 28 × 10 - 3   W / m K

P r = 0,704

Passo 2

Agora que temos as propriedades do ar podemos calcular o número de Rayleigh:

R a L = g β ∆ T L 3 k ρ c p × ϑ

R a L = 9,81 × 1 T - m × T 1 - T 2 × 30 × 10 - 3 3 28 × 10 - 3 1,0849 × 100 7,9 × 1 8,2 × 10 - 6

R a L = 9,81 × 1 323 × 70 - 30 × 30 × 10 - 3 3 28 × 10 - 3 1,0849 × 1007,9 × 18,2 × 10 - 6

R a L = 70383

Vamos agora utilizar a correlação de Nusselt para cavidades retangulares inclinadas para obter o coeficiente convectivo:

N u - L = h - L k = 1 + 1,44 × 1 - 1708 R a L cos ⁡ τ × 1 - 1708 sen ⁡ 1,8 τ 1,6 R a L cos ⁡ τ + R a L cos ⁡ τ 5830 1 3 - 1

h - = k L × 1 + 1,44 × 1 - 1708 R a L cos ⁡ τ × 1 - 1708 sen ⁡ 1,8 τ 1,6 R a L cos ⁡ τ + R a L cos ⁡ τ 5830 1 3 - 1

h - = 28 × 10 - 3 30 × 10 - 3 × 1 + 1,44 × 1 - 1708 70383 × cos ⁡ 60 ° × 1 - 1708 × sen ⁡ 1,8 × 60 ° 1,6 70383 × cos ⁡ 60 ° + 70383 × cos ⁡ 60 ° 5830 1 3 - 1

h - = 2,92   W / m 2 K

Passo 3

Agora que encontramos o coeficiente convectivo podemos calcular a taxa de transferência de calor por convecção natural, aplicando a relação:

q = h - A ( T 1 - T 2 )

q = 2,92 × H × w × ( 70 - 30 )

q = 2,92 × 2 × 2 × ( 70 - 30 )

q = 467,3   W

Resposta

q = 467,3   W .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59 - Vapor de água saturado, a uma pressão absoluta de 4 bar e uma velocidade média de 3m / s , escoa através de uma tubulação horizontal cujos diâmetros interno e externo são de 55 e 65 mm, respectiv
Uma placa, com dimensões de 1 m por 1 m e inclinada com um ângulo de 45°, tem sua superfície inferior exposta a um fluxo térmico radiante líquido de 300 W/m2 . Estando a superfície superior da placa i
Um bastão horizontal com 5 mm de diâmetro está imerso em água mantida a 18°C. Se a temperatura superficial do bastão é de 56°C, estime a taxa de transferência de calor por convecção natural por unidad
Um aquecedor elétrico com a forma de um disco horizontal com 400 mm de diâmetro é usado para aquecer o fundo de um tanque de óleo de motor a uma temperatura de 5°C. Calcule a potência necessária para
Uma tubulação de vapor horizontal, sem isolamento térmico, passa através de uma grande sala cujas paredes e o ar ambiente estão a 300 K. A tubulação, com 150 mm de diâmetro, tem uma emissividade de 0,