Foi proposto usar grandes conjuntos de baterias de lítio recarregáveis para impulsionar veículos elétricos. Nas baterias cilíndricas, cada uma com um raio e comprimento , há reações eletroquímicas exotérmicas enquanto são descarregadas. Como temperaturas excessivamente altas danificam as baterias, propõem-se inseri-las em um material de mudança de fase que se funde quando as baterias se descarregam (e solidifica-se quando as baterias são carregadas; o carregamento está associado a uma reação eletroquímica endotérmica). Considere a parafina dos Problemas e .

(a) Em um instante no tempo durante a descarga da bateria, parafina líquida ocupa uma região anular de raio externo ao redor da bateria, que está gerando de energia térmica. Determine a temperatura na superfície da bateria.

(b) No instante de tempo de interesse na parte (a), qual é a taxa na qual a região anular de líquido está aumentando?

(c) Faça um gráfico da temperatura da superfície da bateria versus o raio externo da região anular ocupada pelo líquido. Explique a relativa insensibilidade da temperatura da superfície da bateria em relação ao tamanho da região anular para .

A primeira coisa a se fazer para determinar é o cálculo do comprimento característico. Para um espaço cilíndrico fechado ele é dado por:

Com o comprimento característico podemos calcular o número de Rayleigh:

O próximo passo antes de calcular é o número de Prandtl:

Agora que temos os adimensionais podemos utilizar a correlação para condutividade efetiva em um espaço fechado cilíndrico:

Vamos agora aplicar este resultado no nosso balanço de energia:

Vamos agora para o item (b). Devido à transferência de calor a parafina começa a derreter e, por isso, a camada de parafina líquida aumenta, ou seja está aumentando. Neste item devemos determinar a taxa em que isso ocorre. Tudo bem?

Vamos começar realizando o balanço de energia na interface entre a parafina líquida e a parafina sólida. Sabemos que chega à interface o calor transferido por convecção externa. Assumindo que não há perdas de energia, todo o calor deve ser utilizado para fundir a parafina. Então:

Rearranjando:

Por fim, vamos ao item (c). Devemos agora fazer um gráfico da temperatura da superfície em relação ao raio externo. Para isso, vamos aplicar as mesmas equações do item (a), porém agora para diversos valores de dentro do intervalo .

Com o auxílio de Excel ou outra ferramenta gráfica podemos realizar os mesmos cálculos do item (a) para outros valores de e, plotar uma função de . Devemos chegar em algo da forma:

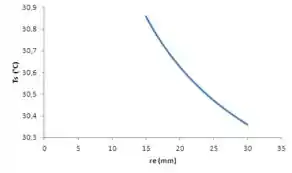
Como podemos ver a temperatura da superfície pouco se alterou neste intervalo de . Isto ocorre porque, com o aumento da raio a área de troca térmica aumenta, o que leva a uma condutividade térmica efetiva maior. Porém, se olharmos a equação de transferência de calor por convecção:

Veremos que aumentar o raio externo leva a ao aumento do termo , o que acarreta em diminuição da troca térmica. Assim, como e aumentam de forma simultânea, a taxa de transferência de calor é pouco afetada e por isso a temperatura da superfície se manteve aproximadamente constante.