O molde usado em um processo de moldagem por injeção é constituído por uma metade superior e uma metade inferior. Cada metade tem e é feita com um metal . O molde frio deve ser aquecido até com água pressurizada (disponível a e com uma vazão total de ) antes da injeção do material termoplástico. A injeção demora somente uma fração de segundo e o molde aquecido () é resfriado em sequência com água fria (disponível a e com uma vazão total de ) antes da ejeção da parte moldada. Após a ejeção, que também demora uma fração de segundo, o processo é repetido.
(a) No projeto convencional do molde, passagens de resfriamento (aquecimento) retas são perfuradas através do molde em um local no qual as passagens não interferem com a parte moldada. Determine as taxas de resfriamento e de aquecimento iniciais do molde, quando cinco passagens com de diâmetro e de comprimento são perfuradas em cada metade do molde (total de passagens). A distribuição de velocidades na água está plenamente desenvolvida na entrada de cada passagem no molde quente (ou frio).
(b) Novos processos de fabricação, conhecidos como fabricação de formas livres seletivas, ou , são usados para construir moldes que são configurados com passagens de resfriamento conformais. Considere o mesmo molde de antes, mas agora com uma passagem curva em forma de serpentina, com 5 mm de diâmetro, projetada no interior de cada metade do molde, fabricada através da. Cada uma das duas passagens em forma de serpentina tem voltas. A passagem em forma de serpentina não interfere na parte moldada. Os canais têm um diâmetro de serpentina . A vazão total da água permanece a mesma da parte (a) Determine as taxas de resfriamento e de aquecimento iniciais do molde.
(c) Compare as áreas superficiais das passagens de resfriamento convencionais e em serpentina. Compare as taxas nas quais a temperatura do molde varia em moldes com passagens de resfriamento/aquecimento convencionais e em serpentina. Qual tipo de passagens de resfriamento, convencional ou em serpentina, irá permitir a produção de uma maior quantidade de peças por dia? Despreze a presença do material termoplástico.
Passo 1
Vamos lá! Nosso problema nos pede as taxas de aquecimento e refrigeração para dois tipos de canais e comparar os processos, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.
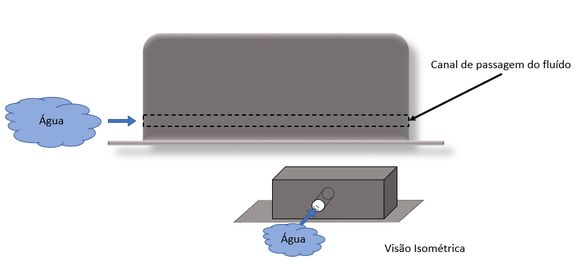
Canal do tipo reto
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá, vamos usar os dados da tabela , para a água à
Para o aquecimento, o número de Reynolds é dado por:
Da relação de , com .
Como , temos que , também precisamos lembrar que a vazão por um canal é um quinto da vazão do sistema, e que o perímetro é dado por , assim:
Como a taxa de calor de cada canal é dada por:
Como temos 5 canais e dois moldes temos que a taxa de calor total para o processo de aquecimento é:
Agora para o resfriamento o número de Reynolds é dado por:
Da equação temos:
Como , temos que , também precisamos lembrar que a vazão por um canal é um quinto da vazão do sistema, e que o perímetro é dado por , assim:
Como a taxa de calor de cada canal é dada por:
Como temos 5 canais e dois moldes temos que a taxa de calor total para o processo de aquecimento é:
Passo 3
(b)
Agora vamos analisar para estrutura dos canais em formato de serpentina, durante o aquecimento temos:
O número critico de Reynolds para a seção espiral é dado pela equação , assim temos:
Como e
O escoamento deverá ser turbulento, vamos usar a relação de , com :
Como , temos que , também precisamos lembrar que a vazão por um canal é um quinto da vazão do sistema, e que o perímetro é dado por , assim:
Como a taxa de calor para os dois moldes é dada por:
Agora para o resfriamento o número de Reynolds é dado por:
Como o , nosso escoamento é laminar, temos:
Como da equação temos:
Assim a equação fica:
Como , temos que , também precisamos lembrar que a vazão por um canal é um quinto da vazão do sistema, e que o perímetro é dado por , assim:
Como a taxa de calor para os dois moldes é dada por:
Passo 4
(c)
Lembrando que é o volume do molde, e cada tipo de estrutura, seja por canais retos ou por serpentina, tem áreas diferentes.
Entretanto vamos fazer os volumes serem os mesmos
Montando uma tabela para os dados temos:
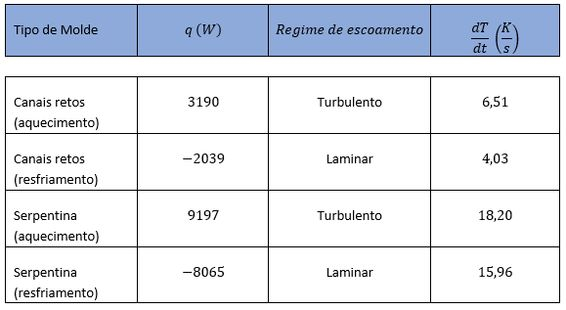
A serpentina acelera os processos de aquecimento de aquecimento e resfriamento por um fator de e para a mesma área, logo é mais efetivo!
Isso é tudo pessoal! \o/

Resposta
(a)
(b)
(c) A serpentina acelera os processos de aquecimento de aquecimento e resfriamento por um fator de e para a mesma área, logo é mais efetivo!