Ar atmosférico a 20°C entra e enche um tanque termicamente isolado, inicialmente evacuado. Usando uma análise de volume de controle da equação 3.63, calcule a temperatura do ar no tanque quando ele estiver cheio.
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é DESENHAR!!!
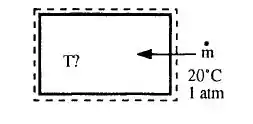
Passo 2
A equação de energia durante o enchimento do tanque adiabático deve respeitar a equação 3.63, que é:
Sabemos que o sistema é adiabático e que não há trabalho de eixo, portanto o lado esquerdo da equação é zerado, beleza?
Passo 3
Abrindo um pouquinho mais nossa equação que sobrou, temos que:
Note que isso é a mesma coisa que escrevermos que:
Porém, como é dado a variação de energia em um sistema como o dado no enunciado? Bem, a gente sabe que o calor que é energia em trânsito, então a quantidade de energia que um corpo ou sistema consegue dar, o outro corpo deve receber essa mesma quantidade. E você vai concordar comigo também que a temperatura do tanque deve ser igual a temperatura do ar que está contido dentro dele, certo?
Portanto,
Onde pela tabela A.2 temos que o k do ar é de 1,4, logo: