Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 48

A água escoa em regime permanente para cima no interior do tubo vertical de 0,1 m de diâmetro e é descarregada para a atmosfera através do bocal que tem 0,05 m de diâmetro. A velocidade média do escoamento na saída do bocal deve ser de 20 m/s. Calcule a pressão manométrica mínima requerida na seção 1. Se o equipamento fosse invertido verticalmente, qual seria a pressão mínima requerida na seção 2 para manter a velocidade na saída do bocal em 20 m/s?

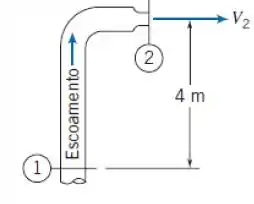
Passo 1

Tá legal! Como nesse caso tudo que entra em 1 deve sair em 2, então teremos a mesma vazão nos dois pontos, sendo assim:

Q 1 = Q 2 → v 1 A 1 = v 2 A 2 → v 1 π D 1 2 4 = v 2 π D 2 2 4 → v 1 = v 2 D 2 D 1 2

Então, substituindo os valores conhecidos, temos:

v 1 = 20 0,05 0,1 2 → v 1 = 5   m / s

Passo 2

Agora vamos aplicar a equação de Bernoulli entre os pontos 1 e 2:

p 1 ρ + v 1 2 2 + g z 1 = p 2 ρ + v 2 2 2 + g z 2

Vamos considerar p 2 = p a t m = 0 , então encontraremos uma pressão p 1 manométrica, dessa forma, substituindo os valores conhecidos, temos:

p 1 999 + 5 2 2 + g 0 = 0 ρ + 20 2 2 + 9,81 4 → p 1 = 226513,3   P a → p 1 = 226,5   k P a

Passo 3

Agora vamos considerar o caso onde o equipamento é invertido verticalmente e vamos aplicar Bernoulli novamente entre os pontos 1 e 2:

p 1 ρ + v 1 2 2 + g z 1 = p 2 ρ + v 2 2 2 + g z 2

Vamos considerar p 1 = p a t m = 0 , então encontraremos uma pressão p 2 manométrica (note que p 2 agora está na outra ponta do dispositivo, dessa forma, substituindo os valores conhecidos, temos:

0 ρ + 20 2 2 + 9,81 ( - 4 ) = p 2 ρ + 5 2 2 + g 0 → p 2 = 148111,7   P a → p 2 = 148,1   k P a

Resposta

p 1 = 226,5   k P a

p 2 = 148,1   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água subterrânea está sendo bombeada para uma piscina cuja seção transversal tem 3m× 4m enquanto a água é descarregada através de um orifício com 5c m de diâmetro à velocidade média constante de 5m /
Uma bomba de 7hp (eixo) é usada para elevar a água até 15m de altura. Se a eficiência mecânica da bomba for de 82 % , determine a vazão de volume máxima da água.
A água escoa a uma vazão de 0,035m 3 / s em um tubo horizontal cujo diâmetro é reduzido de 15c m para 8c m por um redutor. Se a pressão no eixo central for medida como 470 k P a e 440 k P a antes e de
Um tanque grande inicialmente está preenchido com água até 2m acima do centro de um orifício com diâmetro de 10c m e ponta afiada. A superfície da água do tanque é aberta para atmosfera e o orifício d
O perfil de velocidade de escoamento turbulento em um tubo circular é aproximado por u r = u m á x 1 - r R 1 / n á , onde n = 7 . Determine o fator de correção da energia cinética para esse escoamento