Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 113

Um automóvel tem massa de 1.000 kg e área de arrasto CAA 5 0,7 m2. A resistência de rolagem de 70 N é aproximadamente constante. O carro está se movendo em ponto morto, sem freios, a 90 km/h, quando começa a subir uma ladeira de 10% de inclinação (inclinação 5 tan21 0,1 5 5,71). Que distância o carro percorrerá na ladeira até parar?

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos um carro de massa m = 1000   k g e uma área de arrasto de C A A = 0,7   m ² e uma resistência a rolagem F r o l = 70   N . O carro está se movendo a uma velocidade V 0 = 90 k m h = 25   m / s e subindo uma ladeira com inclinação θ = 5,71   ° .

O enunciado nos pede então pra calcular a distância que o carro vai percorrer na ladeira até parar, ou seja, até sua velocidade ser igual a zero. Pra isso, vamos fazer um balanço de forças no carro.

Mas antes da gente ir pro Passo 2, vamos lembrar que para o ar à temperatura ambiente, a massa específica do ar será ρ = 1,2 k g m 3 e sua viscosidade μ = 1,8 × 10 - 5 P a ∙ s .

Agora sim, vem comigo pra gente matar esse problema juntos!

Passo 2

Em primeiro lugar, vamos fazer um balanço das forças agindo no carro olhando pra imagem abaixo:

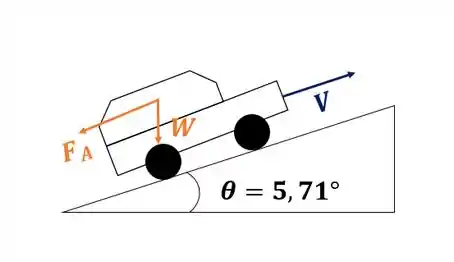
Temos então a força peso agindo numa componente W sen ⁡ θ , além da força de arrasto F A e do atrito F r o l . Isso nos deixa com o seguinte balanço de forças:

m d V d t = - W sen ⁡ θ - F A - F r o l

E onde a força de arrasto é dada por:

F A = C A A ρ V 2 2

Substituindo esta última equação na primeira, teremos:

m d V d t = - W sen ⁡ θ - F r o l - C A A ρ V 2 2

Pra resolver essa EDO, devemos separar as variáveis e integrar a velocidade de V 0 a uma velocidade V e o tempo de t = 0 até um tempo t qualquer:

- ∫ 0 t d t = d V ( W sen ⁡ θ + F r o l ) / m + C A A ρ / 2 m V ²

Resolvendo essa integral, iremos obter:

V = 2 W sen ⁡ θ + F r o l C A A ρ tg ⁡ tg - 1 ⁡ V 0 1 2 C A A ρ W sen ⁡ θ + F r o l - t W sen ⁡ θ + F r o l m 1 2 C A A ρ W sen ⁡ θ + F r o l

E, por fim, pra achar a distância ∆ x na qual o carro para, devemos integrar essa expressão da velocidade no tempo:

∆ x = ∫ 0 t V d t = m ρ C A A ln ⁡ 1 + V 0 2 2 C A A ρ W sen ⁡ θ + F r o l

E agora temos uma expressão pra calcular ∆ x .

Passo 3

Pra finalizar a questão, basta substituir as grandezas que foram definidas no enunciado na expressão que deduzimos no passo anterior.

Primeiro, vamo calcular o peso:

W sen ⁡ θ = 1000   k g 9,81 m s 2 sen ⁡ 5,71 ° = 976   N

Finalmente calculando ∆ x :

∆ x = 1000   k g 1,2 k g m 3 0,7   m 2 ln ⁡ 1 + 25 m s 2 2 0,7   m ² 1,2 k g m 3 976   N + 70   N  

∆ x = 266   m

Pronto, matamos a questão juntos!

Resposta

O carro percorrerá ∆ x = 266   m na ladeira até parar

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O avião Beechcraft T-34C tem um peso global de 24500 N, uma área de asa de 5,6 m² e voa a 518 km/h a 3000 m de altitude padrão. É movido por um propulsor que fornece 300 hp para o ar. Admita neste pro
Reconsidere os dados de sustentação-arrasto para o aerofólio NACA 4412 do problema P8.83. (a) De novo, desenho o diagrama polar sustentação-arrasto e compare qualitativamente com a figura 7.26b. (b) E
Um anemômetro de conchas usa duas semiesferas ocas de 5 cm de diâmetro conectadas a barras de 15 cm, como na Figura P7.91. O arrasto nas barras é desprezível, e o rolamento central tem um torque resis
Hoerner [Referência 12, p. 3-25] especifica que o coeficiente de arrasto de uma bandeira de razão de aspecto de 2:1 é 0,11, com base na área planificada. A Universidade de Rhode Island tem um mastro d
Um automóvel de 1.500 kg utiliza sua área de arrasto CAA = 0,4 m2, além de freios e paraquedas, para reduzir a velocidade de 50 m/s. Seus freios aplicam 5.000 N de resistência. Admita ar padrão ao nív