Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 110
Um arremessador (pitcher) de beisebol arremessa uma “bola com efeito” à velocidade inicial de 105 km/h e uma rotação de 6.500 rpm em torno de um eixo vertical. Uma bola de beisebol pesa 1,42 N e tem um diâmetro de 74 mm. Usando os dados da Figura P7.108 para escoamento turbulento, avalie quanto essa “bola com efeito” terá desviado de sua trajetória em linha reta quando atingir a base do batedor, a 18,44 m de distância.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma bola de beisebol girando a uma velocidade angular de . Ela parte a uma velocidade inicial .
A bola tem peso e diâmetro e descreve uma trajetória horizontal de
Vamos considerar que essa bola descreve uma seção circular de ângulo e raio , que pode ser enxergada no esquema abaixo que fizemos pra te orientar:
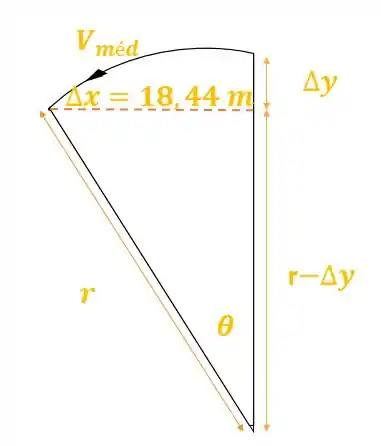
Sendo a velocidade média da bola indo de até o momento que ela cai no chão.
O enunciado nos pede pra calcular a distância na direção percorrida por essa bola, e pra isso nós vamos usar suas forças de arrasto e sustentação.
Antes de irmos para os próximos passos, temos que lembrar que as propriedades do ar a temperatura ambiente são e .
Então vem comigo pra gente resolver esse problema juntos!
Passo 2
Pra resolver o problema, devemos ir na Figura P7.108 pra calcular os coeficientes de arrasto e sustentação pra bola em movimento.
Pra isso, vamos calcular o valor pro termo de entrada :
Agora entramos com esse valor no gráfico da Figura P7.108:
Dessa maneira, encontramos um coeficiente de arrasto e outro de sustentação de, respectivamente, e .
Vamos então calcular as forças de arrasto e de sustentação com base na velocidade inicial :
Passo 3
Agora, vamos calcular as desacelerações horizontal e vertical dessa bola.
A desaceleração horizontal será basicamente dada pela força de arrasto, a que age na direção horizontal:
Já a desaceleração , causada pela força de sustentação será dada por:
Passo 4
Nesse passo, vamos finalizar a questão.
Vamos usar pra calcular a velocidade na qual a bola toca o chão, que ocorre a aproximadamente . Sendo assim, sua velocidade final é aproximadamente de .
Portanto, nossa velocidade média será . Com ela e com aceleração vertical podemos encontrar o raio da seção circular percorrida pela bola:
Agora dê uma olhada na figura exposta no Passo 1. Pra achar o ângulo da seção circular, basta usar fazendo uma simples relação trigonométrica:
E uma relação trigonométrica similar pode ser usada pra encontrar a distância :
Pronto, matamos a questão juntos!
Resposta
A distância percorrida antes que a bola atinja o outro jogador é